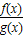练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f′（x）g（x）-f（x）g′（x）=x2（1-x），则函数（ ）
    A．有极大值点1，极小值点0
    B．有极大值点0，极小值点1
    C．有极大值点1，无极小值点
    D．有极小值点0，无极大值点
    【答案】分析：构造函数F（x）=，则由商的导数，可得当x＜0时，F′（x）＞0，0＜x＜1时，F′（x）＞0，x＞1时，F′（x）＜0，由极值的定义可知，在左右两侧的单调性相反，即左右两侧导数值异号的才为极值点．
    解答：解：构造函数F（x）=，则由商的导数，可得F′（x）==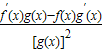
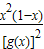
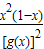    令F′（x）=0，即=0，解得，x=0，或x=1．
    并且当x＜0时，F′（x）＞0，0＜x＜1时，F′（x）＞0，由极值的定义可知，即x=0不是函数F（x）的极值点；
    同理，可得当x＞1时，F′（x）＜0，由极值的定义可知，x=1是函数F（x）的极大值点．
    故选C
    点评：本题为极值点的判断，需构造函数，利用商的导数，结合极值的定义可得答案，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（x）=（x-1）2，g（x）=4x-4数列{an}满足a1=2，（an+1-an）g（an）+f（an）=0，（n∈N+）
    （1）证明数列{an-1}是等比数列；
    （2）设bn=7f（an）-g（an+1），求数列{bn}的前n项和Sn；
    （3）在（2）的条件下，是否存在自然数M使得Sn＜M＜f（x）-g（x）+
    232
    对任意n∈N*和任意实数x均成立，若存在求出满足条件的所有自然数M．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题：
    ①已知f(x)+2f(
    1
    x
    )=3x    ，则函数g（x）=f（2x）在（0，1）上有唯一零点；
    ②对于函数f(x)=x
    1
    2
    的定义域中任意的x1、x2（x1≠x2）必有f(
    x1+x2
    2
    )＜
    f(x1)+f(x2)
    2
    ；
    ③已知f（x）=|2-x+1-1|，a＜b，f（a）＜f（b），则必有0＜f（b）＜1；
    ④已知f（x）、g（x）是定义在R上的两个函数，对任意x、y∈R满足关系式f（x+y）+f（x-y）=2f（x）•g（y），且f（0）=0，但x≠0时f（x）•g（x）≠0．则函数f（x）、g（x）都是奇函数．
    其中正确命题的序号是
    ①③
    ①③
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）=2x，g（x）=3x．
    （1）当x为何值时，f（x）=g（x）？
    （2）当x为何值时，f（x）＞1？f（x）=1？f（x）＜1？
    （3）当x为何值时，g（x）＞3？g（x）=3？g（x）＜3？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x2-alnx，x∈（1，2），
    （1）判断函数f（x）的单调性；
    （2）若f（x）在（1，2）为增函数，g(x)=x-a
    		x
    在（0，1）上为减函数．
    求证：方程f（x）=g（x）+2在（0，+∞）内有唯一解；
    （3）当b＞-1时，若f(x)≥2bx-
    1
    x2
    在x∈（0，1）内恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省厦门市双十中学高二（上）期中数学试卷（理科）（解析版） 题型：解答题

    已知f（x）=（x-1）2，g（x）=4x-4数列{an}满足a1=2，（an+1-an）g（an）+f（an）=0，（n∈N+）
    （1）证明数列{an-1}是等比数列；
    （2）设bn=7f（an）-g（an+1），求数列{bn}的前n项和Sn；
    （3）在（2）的条件下，是否存在自然数M使得Sn＜M＜f（x）-g（x）+对任意n∈N*和任意实数x均成立，若存在求出满足条件的所有自然数M．

    查看答案和解析>>

    同步练习册答案