
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.
【答案】(1) ξ的分布列为
ξ | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
P |
|
|
|
|
|
|
|
(2) 这两台打印机正常使用五年所需购买墨盒的费用的期望为6614元.
【解析】试题分析:(1) ![]() , 一台打印机在5年内消耗墨盒数为22,23,24,25的概率分别为
, 一台打印机在5年内消耗墨盒数为22,23,24,25的概率分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() , 且每台机消耗墨盒数发生的事件是相互独立事件,由此可得每个取值的概率值,进而得到分布列;(2) 记
, 且每台机消耗墨盒数发生的事件是相互独立事件,由此可得每个取值的概率值,进而得到分布列;(2) 记![]() 表示在题设条件下,购买2台新机使用五年在消耗墨盒上所需的费用,若在购买两台新机时,每台机随机购买23盒墨,则需付款
表示在题设条件下,购买2台新机使用五年在消耗墨盒上所需的费用,若在购买两台新机时,每台机随机购买23盒墨,则需付款![]() ,则
,则![]()
试题解析:
(1) ![]()
由题设可知,一台打印机在5年内消耗墨盒数为22,23,24,25的概率分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
且每台机消耗墨盒数发生的事件是相互独立事件.故
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
故ξ的分布列为
ξ | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
P |
|
|
|
|
|
|
|
(2)记![]() 表示在题设条件下,购买2台新机使用五年在消耗墨盒上所需的费用(单位:元)
表示在题设条件下,购买2台新机使用五年在消耗墨盒上所需的费用(单位:元)
若在购买两台新机时,每台机随机购买23盒墨,则需付款
![]()
则![]()
![]()
答:这两台打印机正常使用五年所需购买墨盒的费用的期望为6614元.


科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C是△ABC的三个内角.
(1)3cos(B﹣C)﹣1=6cosBcosC,求cosA的值;
(2)若sin(A+ ![]() )=2cosA,求A.
)=2cosA,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的直角坐标方程,并且用
的直角坐标方程,并且用![]() (
(![]() 为直线的倾斜角,
为直线的倾斜角, ![]() 为参数)的形式写出直线
为参数)的形式写出直线![]() 的一个参数方程;
的一个参数方程;
(2) ![]() 与
与![]() 是否相交,若相交求出两交点的距离,若不相交,请说明理由.
是否相交,若相交求出两交点的距离,若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 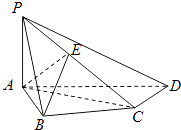
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE; 
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com