
 ,由圆周公式2πR可算出底面周长.
,由圆周公式2πR可算出底面周长. =(0,-acos60°,-asin60°).
=(0,-acos60°,-asin60°).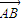 =(x,y,-asin60°).所以
=(x,y,-asin60°).所以 .又由
.又由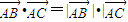 |•cos45°,知-acos60°•y+a2sin60°=a,平方整理得
|•cos45°,知-acos60°•y+a2sin60°=a,平方整理得 ,由此知点B的轨迹.
,由此知点B的轨迹.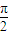 ).设B(x,y,0),则(6分)
).设B(x,y,0),则(6分) =(0,-acosφ,-asinφ).
=(0,-acosφ,-asinφ). =(x,y,-asinφ).所以
=(x,y,-asinφ).所以 φ.由
φ.由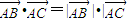 |•cosθ=a•
|•cosθ=a•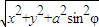 •cosθ.知cos2θ•x2+(cos2θ-cos2φ)y2+a2ysinφsin2φ+a2sin2φ(cos2θ-sin2φ)=0.故当φ=
•cosθ.知cos2θ•x2+(cos2θ-cos2φ)y2+a2ysinφsin2φ+a2sin2φ(cos2θ-sin2φ)=0.故当φ= 时,点B的轨迹为圆;当θ<φ<
时,点B的轨迹为圆;当θ<φ<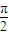 时,点B的轨迹为椭圆;当θ=φ<
时,点B的轨迹为椭圆;当θ=φ< 时,点B的轨迹为抛物线;当θ>φ时,点B的轨迹为双曲线.
时,点B的轨迹为抛物线;当θ>φ时,点B的轨迹为双曲线. ,
, π; (2分)
π; (2分)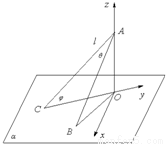
 =(0,-acos60°,-asin60°).
=(0,-acos60°,-asin60°). =(x,y,-asin60°).
=(x,y,-asin60°). .
.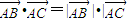 |•cos45°=a•
|•cos45°=a•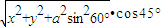 .
. . (11分)
. (11分)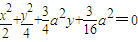 ,
, ).设B(x,y,0),则(6分)
).设B(x,y,0),则(6分) =(0,-acosφ,-asinφ).
=(0,-acosφ,-asinφ). =(x,y,-asinφ).
=(x,y,-asinφ).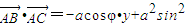 φ.
φ. |•cosθ=a•
|•cosθ=a• •cosθ.
•cosθ. . (11分)
. (11分)
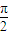 时,点B的轨迹为圆;
时,点B的轨迹为圆; 时,点B的轨迹为椭圆;
时,点B的轨迹为椭圆;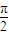 时,点B的轨迹为抛物线;
时,点B的轨迹为抛物线;

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2014届浙江省高二9月质量检测理科数学试卷(解析版) 题型:解答题
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com