
【题目】如图, ![]() 是边长为2的正方形
是边长为2的正方形![]() 的
的![]() 边的中点,将
边的中点,将![]() 与
与![]() 分别沿
分别沿![]() 、
、![]() 折起,使得点
折起,使得点![]() 与点
与点![]() 重合,记为点
重合,记为点![]() ,得到三棱锥
,得到三棱锥![]() .
.
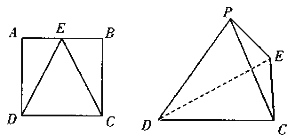
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析: (Ⅰ)由![]() ,
, ![]() ,可得
,可得![]() 平面
平面![]() ,又
,又![]() 在平面
在平面![]() 内,即可证得面面垂直;(Ⅱ)解:设点
内,即可证得面面垂直;(Ⅱ)解:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,根据三棱锥等体积可得
,根据三棱锥等体积可得
![]() ,根据体积公式代入即可求得
,根据体积公式代入即可求得![]() .
.
试题解析:(Ⅰ)证明:∵![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() 交
交![]() 于点
于点![]() ,
, ![]() ,
, ![]() 在平面
在平面![]() 内,∴
内,∴![]() 平面
平面![]() ,
,
∵![]() 在平面
在平面![]() 内,∴平面
内,∴平面![]() 平面
平面![]() .
.
(Ⅱ)解:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
依题意可知,三角形![]() 是底边长为2,高为2的三角形,
是底边长为2,高为2的三角形,
所以其面积为![]() .
.
由(Ⅰ)知![]() 平面
平面![]() ,易知
,易知![]() 是边长为2的等边三角形,其面积为
是边长为2的等边三角形,其面积为![]() ,
, ![]() ,
,
所以![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
点睛:本题考查面面垂直的判定以及等体积法求点线距,属于中档题目. 两平面垂直的判定有两种方法:(1)两个平面所成的二面角是直角;(2)一个平面经过另一平面的垂线.掌握基本的判定和性质定理外还应理解线线、线面、面面垂直的转化思想,逐步学会综合运用数学知识分析解决问题的能力.


科目:高中数学 来源: 题型:
【题目】如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ. 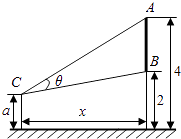
(1)若a=1.5,问:观察者离墙多远时,视角θ最大?
(2)若tanθ= ![]() ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
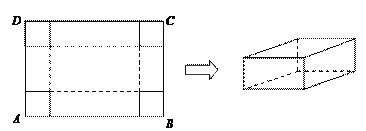
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校餐厅每天供应500名学生用餐,每星期一有A、B两种菜可供选择.调查表明,凡是在这星期一选A种菜的,下星期一会有20%改选B种菜;而选B种菜的,下星期一会有30%改选A菜.用an , bn分别表示在第n个星期选A的人数和选B的人数,若a1=300,则a20=( )
A.260
B.280
C.300
D.320
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com