
【题目】已知椭圆![]() ,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为
,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为![]() 的正方形.
的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(均不在
两点(均不在![]() 轴上),点
轴上),点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率成等比数列,且
的斜率成等比数列,且![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为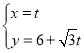 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
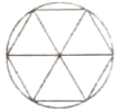
【题目】刘徽(约公元225年—295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术的核心思想是将一个圆的内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,这
变得很大时,这![]() 个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计
个等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中![]() 表示这些半音的频率,它们满足
表示这些半音的频率,它们满足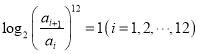 .若某一半音与
.若某一半音与![]() 的频率之比为
的频率之比为![]() ,则该半音为( )
,则该半音为( )
频率 |
|
|
|
|
|
|
|
|
|
|
|
| |
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中数学 来源: 题型:
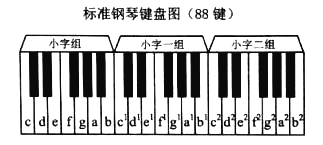
【题目】音乐是用声音来表达人的思想感情的一种艺术,明代的律学家朱载堉创建了十二平均律,并把十二平均律计算得十分精确,与当今的十二平均律完全相同,其方法是将一个八度音程(即相邻的两个具有相同名称的音之间,如图中88键标准钢琴键盘的一部分中,c到c1便是一个八度音程)均分为十二等分的音律,如果用正式的音乐术语称呼原来的7个音符,分别是c,d,e,f,g,a,b,则多出来的5个音符为c#(读做“升c”),d#,f#,g#,a#;12音阶为:c,c#,d,d#,e,f,f#,g,g#,a,a#,b,相邻音阶的频率之比为1:![]() .如图,则键盘c和d的频率之比为
.如图,则键盘c和d的频率之比为![]() 即1:
即1:![]() ,键盘e和f的频率之比为1:
,键盘e和f的频率之比为1:![]() ,键盘c和c1的频率之比为1:2,由此可知,图中的键盘b1和f2的频率之比为( )
,键盘c和c1的频率之比为1:2,由此可知,图中的键盘b1和f2的频率之比为( )
A.![]() B.1:
B.1:![]() C.
C.![]() :1D.
:1D.![]() :1
:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=sinωx(ω>0)向左平移![]() 个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)在(0,2π)上有且只有3个极大值点,f(x)在(0,2π)上有且只有2个极小值点
C.f(x)在![]() 上单调递增
上单调递增
D.ω的取值范围是[![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
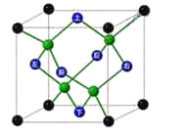
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com