
(12分)
已知四棱锥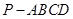 中,
中,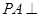 平面
平面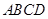 ,底面
,底面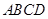 是直角梯形,
是直角梯形,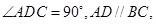
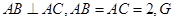 为
为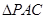 的重心,
的重心,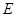 为
为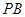 的中点,
的中点,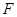 在
在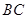 上,且
上,且 ;
;

(1)求证: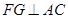 ;
;
(2)当二面角 的正切值为多少时,
的正切值为多少时,
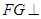 平面
平面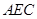 ;
;
(3)在(2)的条件下,求直线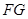 与平面
与平面 所成角
所成角
的正弦值;
(1)略
(2) 当二面角P-CD-A的正切值为2时,FG⊥平面AEC
(3) 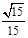
【解析】(1)连结CG并延长交PA于H,连结BH
∵G是△PAC的重心 ∴CG:GH=2:1
∵CF:FB=2:1 ∴CG:GH=CF:FB ∴FG∥BH
∵PA⊥平面ABCD ∴PA⊥AC ∴AC⊥平面PAB
∴ AC⊥BH ∵FG∥BH ∴FG⊥AC ------------4分
(2)如图所示,以A为坐标原点建立空间直角坐标系

∵AB=AC=2且AB⊥AC ∴∠ACB=45° 在直角梯形ABCD中
∵∠BCD=90° ∴∠ACD=45°∵AC=2 ∴AD=CD=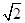
∵PA⊥平面ABCD ∴PA⊥CD ∵CD⊥AD ∴CD⊥平面PAD
∴CD⊥PD ∴∠PDA为二面角P-CD-A的平面角
∴A(0,0,0) C(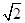 ,
,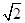 ,0) D(0,
,0) D(0,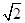 ,0) B(
,0) B(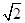 ,
,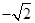 ,0)
,0)
设P(0,0, ) ∴H(0,0,
) ∴H(0,0,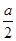 ) E(
) E(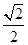 ,
,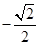 ,
,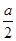 )
)
∵FG⊥平面AEC ∴FG⊥AE∵FG∥BH ∴BH⊥AE
∴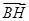 =(
=(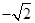 ,
,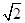 ,
,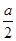 )
) 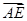 =(
=(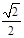 ,
,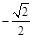 ,
,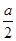 )
)
∴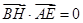 ∴
∴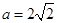 ∴PA=
∴PA=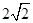
∴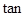 ∠PDA=2 ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分
∠PDA=2 ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ------8分
(3)∵BH∥FG ∴FG与平面PBC所成的角等于BH与平面PBC所成的角
∵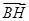 =(
=(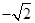 ,
,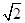 ,
,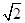 )
) 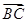 =(0,
=(0,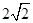 ,0)
,0)
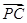 =(
=(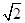 ,
,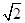 ,
,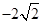 )
)
设平面PBC的法向量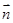 =(x,y,z) ∴
=(x,y,z) ∴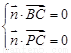 ∴
∴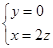 令z=1 ∴
令z=1 ∴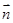 =(2,0,1)
=(2,0,1)
∴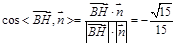 设直线FG与平面PBC所成的角为
设直线FG与平面PBC所成的角为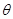
∴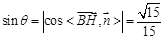 ∴直线FG与平面PBC所成的角的正弦值为
∴直线FG与平面PBC所成的角的正弦值为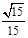 --12分
--12分


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
已知四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() =60
=60![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ∥平面PAE,并给出证明.
∥平面PAE,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2013届新疆乌鲁木齐八中高二上学期期末考试文科数学 题型:解答题
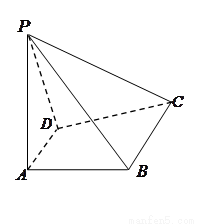
如图,已知四棱锥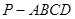 中,
中,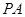 ⊥平面
⊥平面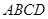 ,
,
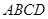 是直角梯形,
是直角梯形,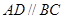 ,
,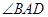
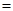 90º,
90º, .
.
(1)求证: ⊥
⊥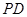 ;
;
(2)在线段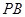 上是否存在一点
上是否存在一点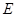 ,使
,使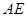 //平面
//平面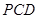 ,
,
若存在,指出点 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
.如图,已知四棱锥![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,
![]() 是直角梯形,
是直角梯形,![]() ,
,![]()
![]() 90º,
90º,![]() .
.
(1)求证:![]() ⊥
⊥![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() //平面
//平面![]() ,
,
若存在,指出点![]() 的位置并加以证明;若不存在,请说明理由
的位置并加以证明;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)已知四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]()
![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ;
;
(1)求证:![]() ;
;
(2)当二面角![]() 的正切值为多少时,
的正切值为多少时,

![]() 平面
平面![]() ;
;
(3)在(2)的条件下,求直线![]() 与平面
与平面![]() 所成角
所成角
的正弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com