
如图,在△![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 成
成![]() 角。
角。
(1)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 边的长。
边的长。

(1)60°(2)![]()
(I)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.
过点A′作A′D⊥AB,垂足为D,则A′D⊥平面ABC,……………………(2分)
∴∠A′ED=30°,又A′O=BO=1,∴∠A′OD=60°,
从而A′D=A′Osin60°=![]() .……………………………………………………(4分)
.……………………………………………………(4分)
过点D作DE⊥BC,垂足为E,连结A′E,据三垂线定理,A′E⊥BC.
∴∠A′ED为二面角A′—BC—A的平面角.……………………………………(5分)
由已知,A′E=1,在Rt△A′DE中![]()
∴∠A′ED=60°故二面角A′—BC—A的大小为60°.…………………………(6分)
(II)设BC=![]() ,∠A′CB=θ,则A′C=
,∠A′CB=θ,则A′C=![]() ,∠OCB=π-θ.
,∠OCB=π-θ.
在Rt△BOC中,![]() …………(8分)
…………(8分)
|
在△A′BC中,A′B2=A′C2+BC2-2A′C·BC![]()
|
![]()
![]() ………………………(12分)
………………………(12分)


科目:高中数学 来源: 题型:
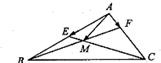 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使| OP |
| OQ |
| OR |
| AM |
| AE |
| AF |
查看答案和解析>>
科目:高中数学 来源: 题型:
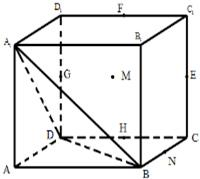 如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )
如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=
如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
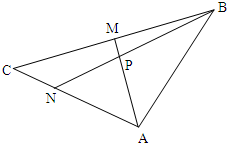 如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且
如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且| AN |
| NC |
| AM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com