【题目】某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）． 
（1）分别写出两种产品的收益与投资额的函数关系式；
（2）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？
【答案】
（1）解：f（x）=k1x，g（x）= 
，
f（1）= 
=k1，g（1）=k2= 
，
∴f（x）= x（x≥0），g（x）= 
（x≥0）
（2）解：设：投资债券类产品x万元，则股票类投资为20﹣x万元．
y=f（x）+g（20﹣x）= 
（0≤x≤20）
令t= 
，则y= 
=﹣ 
．
所以当t=2，即x=16万元时，收益最大，ymax=3万元
【解析】（1）由投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比，结合函数图象，我们可以利用待定系数法来求两种产品的收益与投资的函数关系；（2）由（1）的结论，我们设设投资债券类产品x万元，则股票类投资为20﹣x万元．这时可以构造出一个关于收益y的函数，然后利用求函数最大值的方法进行求解．
科目：高中数学 来源： 题型：
【题目】设函数
.
（1）若
是函数
的极值点，1为函数
的一个零点，求函数
在
上的最小值.
（2）当
时，函数
与
轴在
内有两个不同的交点，求
的取值范围.（其中
是自然对数的底数）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，有两个独立的转盘（
）、（
）．两个图中三个扇形区域的圆心角分别为
、
、
．用这两个转盘进行玩游戏，规则是：依次随机转动两个转盘再随机停下（指针固定不会动，当指针恰好落在分界线时，则这次结果无效，重新开始），记转盘（）指针所对的数为
，转盘（）指针所对的数为
，（、
），求下列概率：
（1）
；
（2）
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩（环）如下：
（1）用茎叶图表示甲、乙两个人的成绩；
（2）根据茎叶图分析甲、乙两人的成绩；
（3）计算两个样本的平均数
和标准差
，并根据计算结果估计哪位运动员的成绩比较稳定．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某农科所发现，一种作物的年收获量 
（单位： 
）与它“相近”作物的株数 
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 
)，并分别记录了相近作物的株数为 
时，该作物的年收获量的相关数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求该作物的年收获量 
关于它“相近”作物的株数
的线性回归方程；
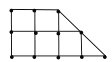
（2）农科所在如图所示的直角梯形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，图中
每个小正方形的边长均为 
，若从直角梯形地块的边界和内部各随机选取一株该作物，求这两株作物 “相
近”且年产量仅相差
的概率．
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估
计分别为,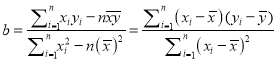 
, 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4
4：坐标系与参数方程
在直角坐标系
中，已知直线l1： 
（
， 
），抛物线C： 
（t为参数）．以原点
为极点， 
轴的非负半轴为极轴建立极坐标系．
（Ⅰ）求直线l1 和抛物线C的极坐标方程；
（Ⅱ）若直线l1 和抛物线C相交于点A（异于原点O），过原点作与l1垂直的直线l2，l2和抛物线C相交于点B（异于原点O），求△OAB的面积的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
