
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 底面ABC.M,N分别为PB,PC的中点.
底面ABC.M,N分别为PB,PC的中点.
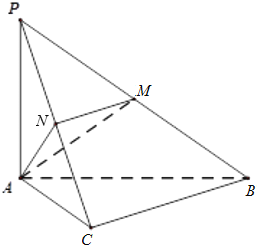
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面PAC;
平面PAC;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为![]() (
(![]() ).
).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与x正半轴、射线![]() (
(![]() )分别交于P,Q两点,当a为何值时,
)分别交于P,Q两点,当a为何值时,![]() 的面积最小?
的面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)在阅读量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人的成绩优秀,在阅量为
人的成绩优秀,在阅量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人成绩不优秀,请完成下面的
人成绩不优秀,请完成下面的![]() 列联表,并判断在“犯错误概率不超过
列联表,并判断在“犯错误概率不超过![]() ”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
阅读量为 | 阅读量为 | 合计 | |
成绩优秀的人数 | |||
成绩不优秀的人数 | |||
合计 |
(2)在抽出的同学中,1)求抽到被污染部分的同学人数;2)从阅读量在![]() 万到
万到![]() 万字及
万字及![]() 万到
万到![]() 万字的同学中选出
万字的同学中选出![]() 人写出阅读的心得体会.求这
人写出阅读的心得体会.求这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研院所共有科研人员800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的240人,无职称的80人,欲了解该科研院所科研人员的创新能力,决定抽取100名科研人员进行调查,应怎样进行抽样?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,D为A1B1的中点,AB=BC=2,
中,D为A1B1的中点,AB=BC=2,![]() ,
,![]() ,则异面直线BD与AC所成的角为( )
,则异面直线BD与AC所成的角为( )

A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)求![]() 与
与![]() 交点的直角坐标;
交点的直角坐标;
(2)过原点![]() 作直线
作直线![]() ,使
,使![]() 与
与![]() ,
, ![]() 分别相交于点
分别相交于点![]() ,
, ![]() (
(![]() ,
, ![]() 与点
与点![]() 均不重合),求
均不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右焦点为
(a>0,b>0)的右焦点为![]() ,右顶点为A,过F作
,右顶点为A,过F作![]() 的垂线与双曲线交于
的垂线与双曲线交于![]() 、
、![]() 两点,过
两点,过![]() 分别作
分别作![]() 的垂线,两垂线交于点
的垂线,两垂线交于点![]() ,若
,若![]() 到直线
到直线![]() 的距离小于
的距离小于![]() , 则双曲线的渐近线斜率的取值范围是
, 则双曲线的渐近线斜率的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com