
已知椭圆 的上、下焦点分别为N、M,若动点
的上、下焦点分别为N、M,若动点 满足
满足

(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)直线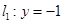 ,设倾斜角为
,设倾斜角为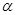 的直线
的直线 过点
过点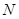 ,交轨迹
,交轨迹 于两点
于两点  ,交直线
,交直线 于点
于点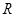 .若
.若 ,求
,求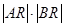 的最小值.
的最小值.
(1)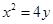 (2)|AR|·|BR|的最小值为
(2)|AR|·|BR|的最小值为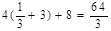 .
.
【解析】
试题分析:(Ⅰ)设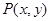 ,则
,则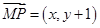 ,
,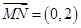 ,
,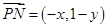 ………2分
………2分
所以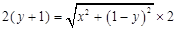 ………4分
………4分
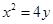 ………6分
………6分
(Ⅱ)设直线l2的方程为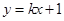 ,与抛物线方程联立消去y得x2-4kx-4=0.
,与抛物线方程联立消去y得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则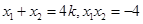 .
………8分
.
………8分
因为直线PA的斜率k≠O,易得点R的坐标为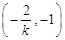 . ………9分
. ………9分
|AR|·|BR|=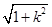 |x1-xR|·
|x1-xR|·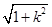 |x2-xR|
|x2-xR|
=(1+k2)·(x1+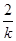 )(x2+
)(x2+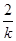 )=(1+k2) x1 x2+(
)=(1+k2) x1 x2+(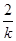 +2 k)( x1+x2)+
+2 k)( x1+x2)+
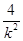 +4
+4
= -4(1+k2)+4k(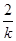 +2k)+
+2k)+ 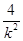 +4=4(k2+
+4=4(k2+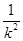 )+8, ………………………13分
)+8, ………………………13分
又α∈(0,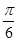 ],k∈(0,
],k∈(0,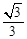 ],
],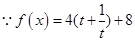 在(0,
在(0,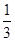 ]递减
]递减
从而|AR|·|BR|的最小值为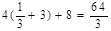 . ………15分
. ………15分
考点:抛物线,直线与抛物线
点评:本试题主要是考查了抛物线方程的求解,以及直线与抛物线的位置关系的运用,对于坐标的表示和运用,是解题的关键,属于中档题。


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
(09年山东实验中学诊断三理)(13分)已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,点
,点![]() 为坐标平面的动点,满足
为坐标平面的动点,满足![]()
![]() (1)求动点
(1)求动点![]() 的轨迹
的轨迹![]() 的方方程;
的方方程;
![]() (2)过点
(2)过点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求直线
,求直线![]() 的方程;
的方程;
![]() (3)在直线
(3)在直线![]() 上是否存在点
上是否存在点![]() ,过该点的坐标:若不存在。试说明理由
,过该点的坐标:若不存在。试说明理由
查看答案和解析>>
科目:高中数学 来源:2013年辽宁省营口市高考数学二模试卷(文科)(解析版) 题型:解答题
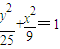 的上、下焦点分别为F2和F1,点A(1,-3),
的上、下焦点分别为F2和F1,点A(1,-3),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com