
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,O为
,O为![]() 的中点.
的中点.
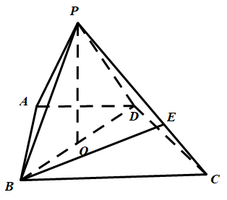
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点F,连接
的中点F,连接![]() ,易得
,易得![]() ,
,![]() ,由线面垂直判定定理可得
,由线面垂直判定定理可得![]() 平面
平面![]() ,进而
,进而![]() ,再将
,再将![]() 与线面垂直判定定理相结合即可得结果.
与线面垂直判定定理相结合即可得结果.
(2)建立如图所示的空间直角坐标系![]() ,可求出平面
,可求出平面![]() 的一个法向量
的一个法向量![]() ,取平面
,取平面![]() 的一个法向量
的一个法向量![]() ,根据图象结合
,根据图象结合![]() 即可得结果.
即可得结果.
(1)证明:取![]() 的中点F,连接
的中点F,连接![]() .
.
因为![]() ,F为
,F为![]() 的中点,所以
的中点,所以![]() .
.
因为O为![]() 中点,F为
中点,F为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,O为
,O为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
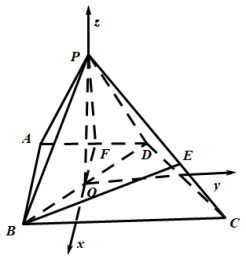
(2)解:以O为坐标原点,![]() 所在直线为x轴,平行
所在直线为x轴,平行![]() 的直线为y轴,
的直线为y轴,![]() 所在直线为z轴建立如图所示的空间直角坐标系
所在直线为z轴建立如图所示的空间直角坐标系![]() ,∵
,∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为![]() ,所以
,所以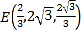 ,
,
故![]() ,
,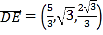 .
.
设平面![]() 的法向量
的法向量![]() ,则
,则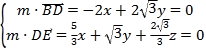
不妨取![]() ,则
,则![]()
平面![]() 的一个法向量
的一个法向量![]() ,记二面角
,记二面角![]() 的大小为
的大小为![]() ,
,
由图可知![]() 为锐角,则
为锐角,则![]() .
.


科目:高中数学 来源: 题型:
【题目】一个盒子中有5只同型号的灯泡,其中有3只一等品,2只二等品,现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(Ⅰ)求第一次取到二等品,且第二次取到的是一等品的概率;
(Ⅱ)求至少有一次取到二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的焦点是
的焦点是![]() ,
,![]() 是抛物线上的点,H为直线
是抛物线上的点,H为直线![]() 上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.
上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线HA,HB与椭圆C的另一交点分别为点D,E,求证:直线DE过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
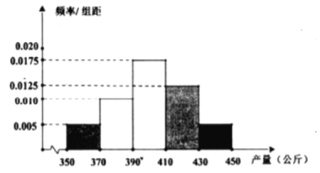
(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: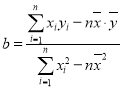 ,
,![]() (回归方程
(回归方程![]() 中)
中)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2,AB=1,E为AD中点,F为CC1中点.
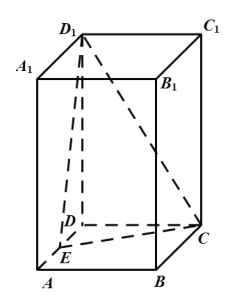
(1)求证:AD⊥D1F;
(2)求证:CE//平面AD1F;
(3)求AA1与平面AD1F成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与![]() 的浓度是否相关,现采集到某城市周一至周五某时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某时间段车流量与![]() 浓度的数据如下表:
浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 39 | 40 | 42 | 44 | 45 |
(1)根据上表数据,求出这五组数据组成的散点图的样本中心坐标;
(2)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若周六同一时间段车流量是100万辆,试根据(2)求出的线性回归方程预测,此时![]() 的浓度是多少?
的浓度是多少?
(参考公式: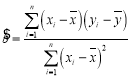 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.
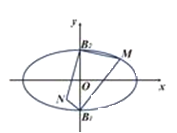
(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在单位正方体![]() 中,点P在线段
中,点P在线段![]() 上运动,给出以下四个命题:
上运动,给出以下四个命题:

![]() 异面直线
异面直线![]() 与
与![]() 间的距离为定值;
间的距离为定值;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;
![]() 异面直线
异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
![]() 二面角
二面角![]() 的大小为定值.
的大小为定值.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com