
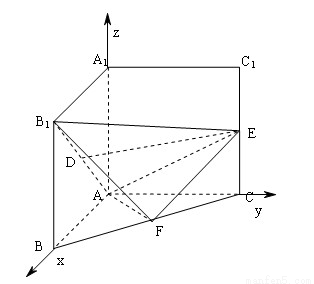
把正方形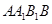 以边
以边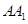 所在直线为轴旋转
所在直线为轴旋转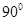 到正方形
到正方形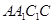 ,其中
,其中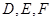 分别为
分别为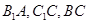 的中点.
的中点.
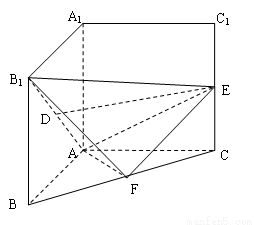
(1)求证: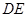 ∥平面
∥平面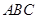 ;
;
(2)求证: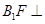 平面
平面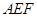 ;
;
(3)求二面角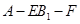 的大小.
的大小.
(1)、(2)见解析;(3)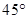 .
.
【解析】本试题主要是考查了空间立体几何中,线面平行的判定和线面垂直的判定以及运用空间向量法,或者几何法求解二面角的综合试题。熟练掌握线面平行和垂直度判定定理和性质定理,是解决该试题的关键。另外求解二面角的思路一般可以借助于三垂线定理来完成。
解:(1)设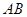 的中点为
的中点为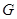 ,连接
,连接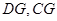
∵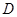 是
是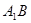 的中点∴
的中点∴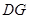 ∥
∥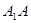 且
且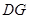
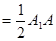 ……………(2分)
……………(2分)
∵ 是
是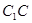 的中点∴
的中点∴ ∥
∥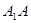 且
且
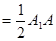 ,∴
,∴ ∥
∥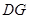 且
且
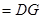
∴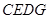 是平行四边形,∴
是平行四边形,∴ ∥
∥
∵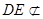 平面
平面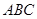 ,
,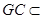 平面
平面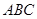 ,∴
,∴ ∥平面
∥平面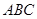 ……………(4分)
……………(4分)
(2) ∵ 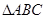 为等腰直角三角形,
为等腰直角三角形,
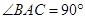 ,且
,且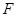 是
是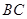 的中点
的中点
∴ 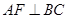 ∵平面
∵平面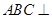 平面
平面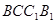 ∴
∴ 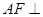 平面
平面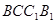
∴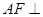
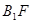 ………………(6分)
………………(6分)
设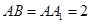 ,则在
,则在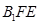 中,
中, ,
,
则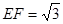 ,
, ∴
∴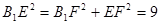
∴ 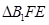 是直角三角形,∴
是直角三角形,∴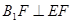
∵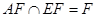 ∴
∴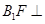 平面
平面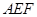 …(8分)
…(8分)
(3)分别以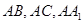 为
为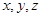 轴建立空间直角坐标系
轴建立空间直角坐标系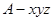 如图,
如图,
设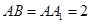 ,则设
,则设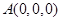 ,
,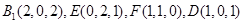 ………(9分)
………(9分)
∵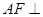 平面
平面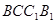 ,∴
面
,∴
面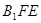 的法向量为
的法向量为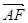 =
=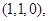 ……………(10分)
……………(10分)
设平面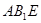 的法向量为
的法向量为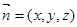 ,∵
,∵ 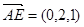 ,
, 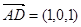
∴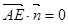 ,
,
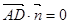 ,
∴
,
∴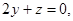 ,
,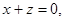
不妨设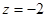 ,可得
,可得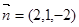 ………………(11分)
………………(11分)
,∴ 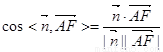 =
=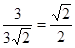
∵ 二面角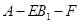 是锐角,∴
二面角
是锐角,∴
二面角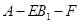 的大小
的大小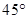 ..........(12分)
..........(12分)


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
 如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路l(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数y=-x2+2(0≤x≤
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路l(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数y=-x2+2(0≤x≤| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路l(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数y=-
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路l(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
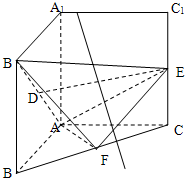 (2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.
(2012•平遥县模拟)把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高三3月月考数学试卷(解析版) 题型:解答题
(本小题满分15分)
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.

(1)当 时,求直路
时,求直路 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com