
【题目】已知函数![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若对任意的![]() ,
,![]() 恒有
恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,递减区间为
时,递减区间为![]() ,当
,当![]() 时,递减区间为
时,递减区间为![]() ,递增区间为
,递增区间为![]() ,当
,当![]() 时,递减区间为
时,递减区间为![]() ,递增区间为
,递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先对函数求导,然后求得导数等于零的方程的根,从而根据根的大小分![]() 、
、![]() 、
、![]() ;(2)首先结合(1)将问题转化为
;(2)首先结合(1)将问题转化为![]() ,然后根据函数的单调性求得
,然后根据函数的单调性求得![]() 的最小值,由此求得实数
的最小值,由此求得实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在定义域
在定义域![]() 单调递减;
单调递减;
当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() ,
,![]() 单调递减,
单调递减,
在区间![]() 上
上![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,在区间
时,在区间![]() ,
,![]() 上
上![]() ,
,![]() 单调递减,
单调递减,
在区间![]() 上
上![]() ,
,![]() 单调递增.
单调递增.
故![]() 时,递减区间为
时,递减区间为![]() ;
;
![]() 时,递减区间为
时,递减区间为![]() ,
,![]() ,递增区间为
,递增区间为![]() ;
;
![]() 时,递减区间为
时,递减区间为![]() ,
,![]() ,递增区间为
,递增区间为![]() .………………6分
.………………6分
(2)由(1)知当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递减;
单调递减;
所以当![]() 时,
时,![]() ,
,![]() ,
,
问题等价于:对任意的![]() ,
,
恒有![]() 成立,即
成立,即![]() ,
,
因为![]() ,∴
,∴![]() .
.
所以,实数![]() 的取值范围是
的取值范围是![]() .………………12分
.………………12分


科目:高中数学 来源: 题型:
【题目】(必须列式,不能只写答案,答案用数字表示)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)求共有多少种放法;
(2)求恰有一个盒子不放球,有多少种放法;
(3)求恰有两个盒内不放球,有多少种放法;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
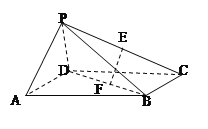
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
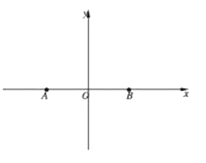
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com