（08年鹰潭市二模理）（12分）如图，正方形
所在的平面与平面
垂直，
是
和
的交点，
，且
．
(Ⅰ)求证：
平面
；
(Ⅱ)求直线
与平面所成的角的大小；
(Ⅲ)求二面角
的大小．
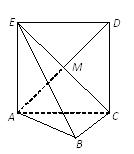
解析:解法一：(Ⅰ)∵四边形
是正方形，
． ………………………1分
∵平面
平面
，
又∵
，
平面
．……………………3分
平面，
．
平面
． ………………4分
(Ⅱ)连结
，
平面，
是直线
与平面
所成的角．……………………5分
设
，则
，
， ……………………6分
，
．
即直线与平面所成的角为
． …………………8分
(Ⅲ)过
作
于
，连结
． …………………………9分
平面，
．
平面
．
是二面角
的平面角．…………………10分
∵平面平面，
平面．
．
在
中， ，有
．
由(Ⅱ)所设可得
，
，
．………………………11分
．
．
∴二面角等于
． ………………………12分
解法二: ∵四边形是正方形 ，
，∵平面平面，
平面， ……………………2分
∴可以以点为原点，以过点平行于
的直线为
轴，分别以直线
和
为
轴和
轴，
建立如图所示的空间直角坐标系
．
设
，则
，
是正方形的对角线的交点，
．……………………4分
(Ⅰ)
，
，
，
，…………………………5分
平面． ……………………6分
(Ⅱ) 平面，
为平面的一个法向量，………………………7分
，
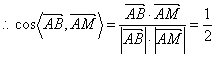．………………………8分
．
∴直线与平面所成的角为．……………………9分
(Ⅲ) 设平面
的法向量为
，则
且
，
且
．
即
取
，则
， 则
．……………………10分
又∵
为平面的一个法向量，且
，
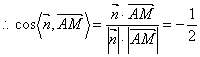，……………………11分
设二面角的平面角为
，则
，
．
∴二面角等于．…………………………………12分
科目：高中数学 来源： 题型：
（08年鹰潭市二模理）（14）设关于x的方程
有两个实根
、
，且
.定义函数
（Ⅰ）求
的值；（Ⅱ）判断
在区间
上的单调性，并加以证明；
（Ⅲ）若
为正实数，证明不等式：
查看答案和解析>>
科目：高中数学 来源： 题型：
（08年鹰潭市二模理）（12分） 已知O为坐标原点，点E、F的坐标分别为
、
，动点A、M、N满足
（
），
，
，
．
（Ⅰ）求点M的轨迹W的方程；
（Ⅱ）点
在轨迹W上，直线PF交轨迹W于点Q，且
，若
，求实数
的范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
（08年鹰潭市二模理）（12分） 已知向量
, 
分别为△ABC的三边a，b，c所对的角.
（Ⅰ）求角C的大小;
（Ⅱ）若sinA, sinC, sinB 成等比数列, 且
, 求c的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
；
，求