(1)解:∵以原点为圆心,椭圆的短半轴为半径的圆与直线
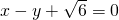
相切,
∴b=
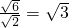
,
∵椭圆

的离心率为

,
∴
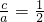
∴
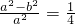
,∴
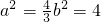
,
∴椭圆C的方程为

(2)证明:设A(x
0,y
0),B(x
0,-y
0)
将直线PB:y=
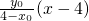
代入椭圆

,可得[3+
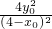
]x
2-
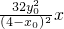
+
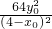
-12=0
设E(x
1,y
1),则x
1+x
0=
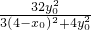
=
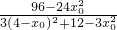
=
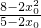
∴
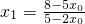
,∴y
1=
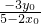
∴直线AE:
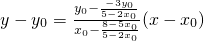
化简可得
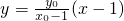
∴直线AE与x轴相交于定点Q:(1,0)
(3)解:由(2)知x
1+x
0=
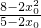
,x
1x
0=
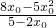
,y
1y
0=
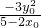
=
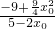
∵
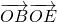
=x
1x
0-y
1y
0,
∴
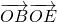
=
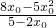
-
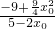
=
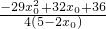
设5-2x
0=t,∵x
0∈(-2,2),∴t∈(1,9)
∴
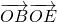
=-
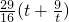
+

∵t∈(1,9),∴
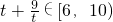
∴
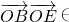
(-4,

]
分析:(1)利用以原点为圆心,椭圆的短半轴为半径的圆与直线
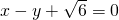
相切,可求b的值,再利用椭圆的离心率为

,即可求出椭圆C的方程;
(2)设A(x
0,y
0),B(x
0,-y
0),将直线PB:y=
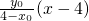
代入椭圆

,可得[3+
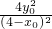
]x
2-
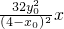
+
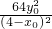
-12=0,从而可得E的坐标,从而可得直线AE的方程,进而可知直线AE与x轴相交于定点Q;
(3)由(2)知x
1+x
0=
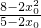
,x
1x
0=
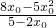
,y
1y
0=
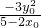
=
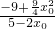
,
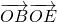
=x
1x
0-y
1y
0,从而可得
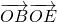
=
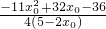
,设5-2x
0=t,进而可确定
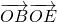
的取值范围.
点评:本题考查椭圆的标准方程,考查直线恒过定点,考查向量知识的运用,同时考查学生分析解决问题的能力与计算能力.

 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线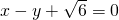 相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交椭圆C于另一点E.
相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交椭圆C于另一点E.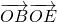 的取值范围.
的取值范围.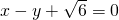 相切,
相切,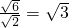 ,
, 的离心率为
的离心率为 ,
,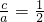
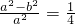 ,∴
,∴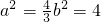 ,
,
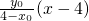 代入椭圆
代入椭圆 ,可得[3+
,可得[3+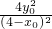 ]x2-
]x2-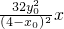 +
+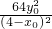 -12=0
-12=0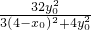 =
=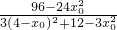 =
=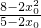
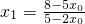 ,∴y1=
,∴y1=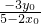
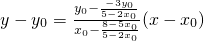
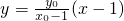
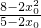 ,x1x0=
,x1x0=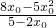 ,y1y0=
,y1y0=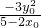 =
=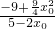
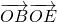 =x1x0-y1y0,
=x1x0-y1y0,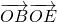 =
=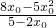 -
-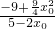 =
=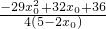
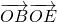 =-
=-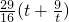 +
+
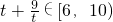
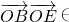 (-4,
(-4, ]
]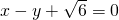 相切,可求b的值,再利用椭圆的离心率为
相切,可求b的值,再利用椭圆的离心率为 ,即可求出椭圆C的方程;
,即可求出椭圆C的方程;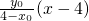 代入椭圆
代入椭圆 ,可得[3+
,可得[3+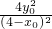 ]x2-
]x2-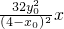 +
+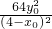 -12=0,从而可得E的坐标,从而可得直线AE的方程,进而可知直线AE与x轴相交于定点Q;
-12=0,从而可得E的坐标,从而可得直线AE的方程,进而可知直线AE与x轴相交于定点Q;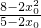 ,x1x0=
,x1x0=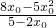 ,y1y0=
,y1y0=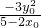 =
=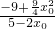 ,
,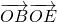 =x1x0-y1y0,从而可得
=x1x0-y1y0,从而可得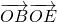 =
=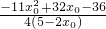 ,设5-2x0=t,进而可确定
,设5-2x0=t,进而可确定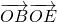 的取值范围.
的取值范围.

 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: