
定义在(-1,1)上的函数f(x)满足①对任意x、y∈(-1,1),都有f(x)+f(y)=f(![]() );②当x∈(-1,0)时,有f(x)>0.
);②当x∈(-1,0)时,有f(x)>0.
求证:![]() .
.
证明略
对f(x)+f(y)=f(![]() )中的x,y,令x=y=0,得f(0)=0,
)中的x,y,令x=y=0,得f(0)=0,
再令y=-x,又得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),
∴f(x)在x∈(-1,1)上是奇函数.
设-1<x1<x2<0,则f(x1)-f(x2)=f(x1)+f(-x2)=f(![]() ),
),
∵-1<x1<x2<0,∴x1-x2<0,1-x1x2>0![]() ∴
∴![]() <0,
<0,
于是由②知f(![]() )?>0,
)?>0,
从而f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在x∈(-1,0)上是单调递减函数.
根据奇函数的图像关于原点对称,知
f(x)在x∈(0,1)上仍是递减函数,且f(x)<0.

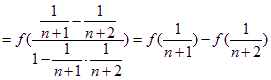
![]()
![]()
![]()
![]()


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4x |
| a |
| 2x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 4x |
| a |
| 2x |
查看答案和解析>>
科目:高中数学 来源:专项题 题型:解答题
 ,
, ;
;查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省宣城市泾县中学高一(上)12月段考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com