
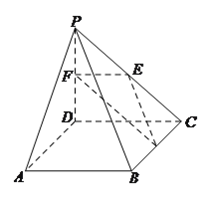
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
【答案】(1)![]() (2)见解析(3)当
(2)见解析(3)当![]() 为线段
为线段![]() 的中点时,满足使
的中点时,满足使![]() 平面
平面![]()
【解析】试题分析:(1)根据线面垂直确定高线,再根据锥体体积公式求体积(2)先寻找线线平行,根据线面平行判定定理得线面平行,最后根据面面平行判定定理得结论(3)由题意可得![]() 平面
平面![]() ,即
,即![]() ,取线段
,取线段![]() 的中点,则有
的中点,则有![]() ,而
,而![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 平面
平面![]()
试题解析:(![]() )解:∵
)解:∵![]() 平面
平面![]() ,
,
∴![]() .
.
(![]() )证明:∵
)证明:∵![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
∴![]() ,
,
由正方形![]() ,
,
∴![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
同理可得: ![]() ,
,
可得![]() 平面
平面![]() ,
,
又![]() ,
,
∴平面![]() 平面
平面![]() .
.
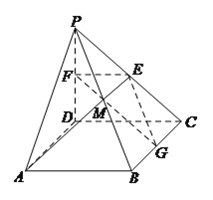
(![]() )解:当
)解:当![]() 为线段
为线段![]() 的中点时,满足使
的中点时,满足使![]() 平面
平面![]() ,
,
下面给出证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,
,
∴四点![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点共面,由
四点共面,由![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() 为等腰三角形,
为等腰三角形, ![]() 为斜边的中点,
为斜边的中点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】某县相邻两镇在一平面直角坐标系下的坐标为A(1,2)、B(4,0),一条河所在直线方程为l:x+2y-10=0,若在河边l上建一座供水站P使之到A、B两镇的管道最省,问供水站P应建在什么地方?此时|PA|+|PB|为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=![]() 且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论:
且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论: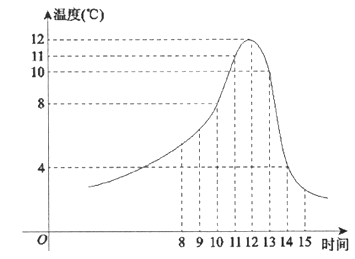
①该食品在6℃的保鲜时间是8小时;
②当x∈[-6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间。
其中,所有正确结论的序号是__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成封闭图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,设p:实数x满足x2﹣4ax+3a2<0,q:实数x满足(x﹣3)2<1.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,且函数
,且函数![]() =
= ![]() 是偶函数
是偶函数
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函数
,求函数![]() 在
在![]() 的最大值和最小值
的最大值和最小值
(3)函数![]() 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com