练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    图中的曲线叫雪花曲线(Koch　Snowflake)，它的生成方法是：

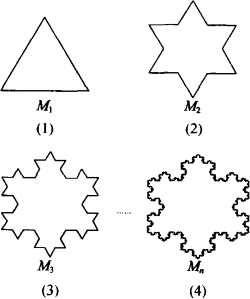
    (1)将正三角形图(1)的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图(2)；

    (2)将图(2)的每边三等分，重复上述的作图方法，得到图(3)；

    (3)再按上述方法继续做下去，就可以得到图(4)所示的曲线．

    将图(1)、(2)、(3)…中的图形依次记作M1、M2、M3、…．

    思考1：请分别说出M1、M2、M3的边数，想一想、如何得到M4的边数？

    思考2：如果知道了Mn－1的边数，我们能否知道Mn的边数？

    答案：
    解析：

    　　思考1：

    　　可以发现M1的一条边都相应变成M2的4条边，即M2的边数是M1的边数的4倍，得M2的边数是12；M2的一条边都相应变成M3的4条边，即M3的边数是M2的边数的4倍，得M3的边数为48；同样M3的每一条边都相应变成M4的4条边，即M4的边数是M3的边数的4倍，得M4的边数为是192．(如图)

    　　思考2：

    　　学生有了对M2、M3、M4的探索经验，在初步形成的等比概念的指导下，结合电脑直观演示，较快地得出Mn的边数是Mn－1的边数的4倍．

    　　若边数为bi(i＝1，2，3，…，n)，则bi+1＝4bi(i＝1，2，3，…，n)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    冬天，洁白的雪花飘落时十分漂亮．为研究雪花的形状，1904年，瑞典数学家科克（Koch Heige Von）把雪花理想化，得到了雪花曲线，也叫科克曲线．它的形成过程如下：
    （i）将正三角形（图①）的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；
    （ii）将图②的每边三等分，重复上述作图方法，得到图③；
    （iii）再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线．
    将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1．
    求：（1）Mn的边数an；
        （2）Mn的边长Ln；
        （3）Mn的面积Sn的极限．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年上海市十四校高三（上）第二次联考数学试卷（理科）（解析版） 题型：解答题

    冬天，洁白的雪花飘落时十分漂亮．为研究雪花的形状，1904年，瑞典数学家科克（Koch Heige Von）把雪花理想化，得到了雪花曲线，也叫科克曲线．它的形成过程如下：
    （i）将正三角形（图①）的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；
    （ii）将图②的每边三等分，重复上述作图方法，得到图③；
    （iii）再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线．
    将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1．
    求：（1）Mn的边数an；
        （2）Mn的边长Ln；
        （3）Mn的面积Sn的极限．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年上海市十四校高三（上）第二次联考数学试卷（文科）（解析版） 题型：解答题

    冬天，洁白的雪花飘落时十分漂亮．为研究雪花的形状，1904年，瑞典数学家科克（Koch Heige Von）把雪花理想化，得到了雪花曲线，也叫科克曲线．它的形成过程如下：
    （i）将正三角形（图①）的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；
    （ii）将图②的每边三等分，重复上述作图方法，得到图③；
    （iii）再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线．
    将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1．
    求：（1）Mn的边数an；
        （2）Mn的边长Ln；
        （3）Mn的面积Sn的极限．

    查看答案和解析>>

    同步练习册答案