练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    过点P(-1,0)作圆C：(x - 1)2 + （y - 2）2 = 1的两切线，设两切点为A、B，圆心为C，则过A、B、C的圆方程是

    A．x2 + (y - 1)2 = 2                  B．x2 + (y - 1)2 = 1 

    C．(x - 1)2 + y2 = 4                          D．(x - 1)2 + y2 = 1

    A 


    解析:

    因为C(1,2)，线段PC的中点M(0,1)就是所求圆的圆心，半径为，所以过A、B、C的圆方程是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年上虞市质检一理） 已知函数(常数t>0)，过点P(1,0)作曲线y=f(x)的两条切线PM、PN，切点分别为M、N.

       (I)求函数的单调递增区间；

       (II)设，试求函数的表达式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

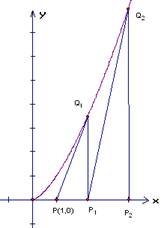
    （08年咸阳市一模） （14分）如图，过点P(1,0)作曲线C: 的切线，切点为,设点在x轴上的投影是点；又过点作曲线C的切线，切点为,设在x轴上的投影是；…；依此下去,得到一系列点,,…,,…,设点的横坐标为.

    （Ⅰ）试求数列｛｝的通项公式；（用的代数式表示）

    （Ⅱ）求证：

    （Ⅲ）求证：（注：）.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届安徽合肥一六八中学高二上学期期中考试文数学卷（解析版） 题型：解答题

    如图，在直角坐标系中，射线OA: x－y=0（x≥0），OB: x+2y=0（x≥0），过点P(1,0)作直线分别交射线OA、OB于A、B两点.

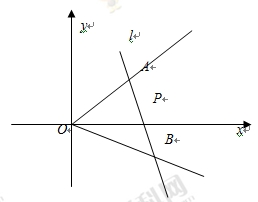
    （1）当AB中点为P时，求直线AB的斜率

    （2）当AB中点在直线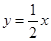上时，求直线AB的方程.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届江西白鹭洲中学高二上学期第三次月考理科数学试题（解析版） 题型：解答题

    在直角坐标系中，射线OA: x－y=0（x≥0），

    OB: x+2y=0（x≥0），过点P(1,0)作直线分别交射线OA、OB于A、B两点.

    （1）当AB中点为P时，求直线AB的方程；

    （2）当AB中点在直线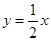上时，求直线AB的方程.

     

    查看答案和解析>>

    同步练习册答案