练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
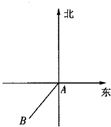
    （2012•河北模拟）已知岛A南偏西38°方向，距岛3海里的B处有一艘缉私艇．岛A处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用0.5小时能截住该走私船？（参考数据：sin38°=
    5
    		3
    14
    ，sin22°=
    3
    		3
    14
    ．）
    分析：在△ABC中，由余弦定理可得BC，从而可求速度，再利用正弦定理，可求∠ABC=38°，进而可求我巡逻艇的航行方向．
    解答：解：由题意AC射线即为走私船航行路线．
    假设我巡逻艇恰在C处截获走私船，我巡逻艇的速度为每小时v海里，则BC=0.5v，AC=5．
    依题意，∠BAC=180°-38°-22°=120°，

    由余弦定理：BC2=AB2+AC2-2AB•ACcos120°，∴BC=7
    ∵BC=0.5v，∴v=14海里/h，
    又由正弦定理，sin∠ABC=
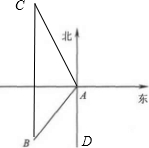
    AC•sin∠BAC
    BC
    =
    5
    		3
    14
    ，∴∠ABC=38°，
    ∵∠BAD=38°，∴BC∥AD
    即我巡逻艇须用每小时14海里的速度向正北方向航行才能恰用0.5小时在C处截住该走私船
    点评：本题以实际问题为素材，考查利用正弦、余弦定理解决三角形问题，解题的关键是构建三角形的模型，合理运用正弦、余弦定理．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•河北模拟）已知函数f（x）=xlnx，g（x）=-x2+ax-2
    （Ⅰ）求函数f（x）在[t，t+2]（t＞0）上的最小值；
    （Ⅱ）若函数y=f（x）+g（x）有两个不同的极值点x1，x2（x1＜x2）且x2-x1＞ln2，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

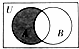    （2012•河北模拟）设全集U=R，A={x|2(x-1)2＜2}，B={x|log
    1
    2
    (x2+x+1)＞-log2(x2+2)    }，则图中阴影部分表示的集合为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•河北模拟）如图是一个程序框图，该程序框图输出的结果是
    4
    5
    ，则判断框内应该填入的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•河北模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其导函数f'（x）的部分图象如图所示，则函数f（x）的解析式为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•河北模拟）定义在[1，+∞）上的函数f（x）满足：①f（2x）=cf（x）（c为正常数）；②当2≤x≤4时，f（x）=1-（x-3）2，若函数f（x）的图象上所有极大值对应的点均落在同一条直线上，则c等于（　　）

    查看答案和解析>>

    同步练习册答案