
【题目】已知椭圆![]() :
:![]() 的焦距为8,其短轴的两个端点与长轴的一个端点构成正三角形。
的焦距为8,其短轴的两个端点与长轴的一个端点构成正三角形。
(1)求![]() 的方程;
的方程;
(2)设![]() 为
为![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于两点
于两点![]() ,
,![]() .
.
(i)证明:![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(ii)当![]() 取最小值时,求点
取最小值时,求点![]() 的坐标。
的坐标。
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知,根据椭圆的焦距为8,其短轴的两个端点与长轴的个端点构成正三角形,求得![]() 的值,即可求得椭圆的方程;
的值,即可求得椭圆的方程;
(2)(ⅰ)设点![]() 的坐标为
的坐标为![]() ,验证当
,验证当![]() 时,
时,![]() 平分
平分![]() 显然成立;当
显然成立;当![]() 由直线
由直线![]() 的方程和椭圆的方程联立方程组,求解
的方程和椭圆的方程联立方程组,求解![]() 中点
中点![]() 的坐标,即可得到结论;
的坐标,即可得到结论;
(ⅱ)由(ⅰ)可知,求得![]() 和
和![]() ,得到
,得到![]() ,利用基本不等式,即可求解.
,利用基本不等式,即可求解.
(1)由已知,得![]() . 因为
. 因为![]() ,易解得
,易解得![]() .
.
所以,所求椭圆![]() 的标准方程为
的标准方程为 ![]()
(2)![]() 设点
设点![]() 的坐标为
的坐标为![]()
当![]() 时,
时,![]() 与
与![]() 轴垂直
轴垂直![]() 为
为![]() 的中点
的中点![]() 平分
平分![]() 显然成立
显然成立
当![]() 由已知可得:
由已知可得:
![]() 则直线
则直线![]() 的方程为:
的方程为:![]()
设![]()
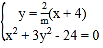 消去
消去![]() 得:
得:
![]() ,
,
![]()
![]()
![]() 中点
中点![]() 的坐标为
的坐标为![]()
又![]() 在直线
在直线![]() 上.
上.
综上![]() 平分线段
平分线段![]()
![]() 当
当![]() 时,
时,![]() 则
则![]()
当![]() 时,由
时,由![]() 可知
可知

![]()
(当且仅当![]() ,即
,即![]() 时等号成立),
时等号成立),
∴点![]() 的坐标为
的坐标为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
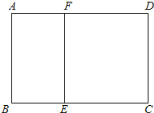
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
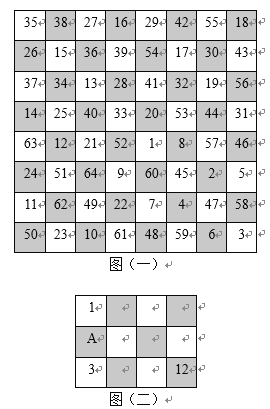
【题目】2018年国际象棋奥林匹克团体赛中国男队、女队同时夺冠.国际象棋中骑士的移动规则是沿着3×2格或2×3格的对角移动.在历史上,欧拉、泰勒、哈密尔顿等数学家研究了“骑士巡游”问题:在![]() 格的黑白相间的国际象棋棋盘上移动骑士,是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格?
格的黑白相间的国际象棋棋盘上移动骑士,是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格?
图(一)给出了骑士的一种走法,它从图上标1的方格内出发,依次经过标2,3,4,5,6,![]() ,到达标64的方格内,不重复地走遍棋盘上的每一格,又可从标64的方格内直接走回到标1的方格内.如果骑士的出发点在左下角标50的方格内,按照上述走法,_____(填“能”或“不能”)走回到标50的方格内.
,到达标64的方格内,不重复地走遍棋盘上的每一格,又可从标64的方格内直接走回到标1的方格内.如果骑士的出发点在左下角标50的方格内,按照上述走法,_____(填“能”或“不能”)走回到标50的方格内.
若骑士限制在图(二)中的3×4=12格内按规则移动,存在唯一一种给方格标数字的方式,使得骑士从左上角标1的方格内出发,依次不重复经过2,3,4,5,6,![]() ,到达右下角标12的方格内,分析图(二)中A处所标的数应为____.
,到达右下角标12的方格内,分析图(二)中A处所标的数应为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com