
【题目】7个人排成一排,按下列要求各有多少种排法?
![]() 其中甲不站排头,乙不站排尾;
其中甲不站排头,乙不站排尾;
![]() 其中甲、乙、丙3人两两不相邻;
其中甲、乙、丙3人两两不相邻;
![]() 其中甲、乙中间有且只有1人;
其中甲、乙中间有且只有1人;
![]() 其中甲、乙、丙按从左到右的顺序排列.
其中甲、乙、丙按从左到右的顺序排列.
【答案】(1) ![]() 种
种![]() (2)
(2)![]() 种 (3)
种 (3)![]() 种 (4)
种 (4)![]() 种
种
【解析】
(1)分别计算甲站在排尾和甲不站在排尾排列数,求和即可;
(2)将除甲、乙、丙之外的4人进行全排列,在5个空位种任选3个,利用插空法计算即可;
(3)先将甲、乙全排列,在剩余的5个人中任选1个,安排在甲乙之间,利用捆绑法计算即可;
(4)在7个位置中任取4个,安排除甲、乙、丙之外的4人,再将这三人按顺序安排剩下三个位置即可.
![]() 根据题意,分2种情况讨论:
根据题意,分2种情况讨论:
![]() 、甲站在排尾,剩余6人进行全排列,安排在其他6个位置,有
、甲站在排尾,剩余6人进行全排列,安排在其他6个位置,有![]() 种排法,
种排法,
![]() 、甲不站在排尾,则甲有5个位置可选,有
、甲不站在排尾,则甲有5个位置可选,有![]() 种排法,
种排法,
乙不能在排尾,也有5个位置可选,有![]() 种排法,
种排法,
剩余5人进行全排列,安排在其他5个位置,有![]() 种排法,
种排法,
则此时有![]() 种排法;
种排法;
故甲不站排头,乙不站排尾的排法有![]() 种
种![]()
![]() 根据题意,分2步进行分析,
根据题意,分2步进行分析,
![]() 、将除甲、乙、丙之外的4人进行全排列,有
、将除甲、乙、丙之外的4人进行全排列,有![]() 种情况,
种情况,
排好后,有5个空位,
![]() 、在5个空位种任选3个,安排甲、乙、丙3人,有
、在5个空位种任选3个,安排甲、乙、丙3人,有![]() 种情况,
种情况,
则共有![]() 种排法
种排法![]()
![]() 根据题意,
根据题意,
![]() 、先将甲、乙全排列,有
、先将甲、乙全排列,有![]() 种情况,
种情况,
![]() 、在剩余的5个人中任选1个,安排在甲乙之间,有
、在剩余的5个人中任选1个,安排在甲乙之间,有![]() 种选法,
种选法,
![]() 、将三人看成一个整体,与其他四人进行全排列,有
、将三人看成一个整体,与其他四人进行全排列,有![]() 种排法,
种排法,
则甲、乙中间有且只有1人共有![]() 种排法
种排法![]()
![]() 根据题意,分2步进行
根据题意,分2步进行
![]() 、在7个位置中任取4个,安排除甲、乙、丙之外的4人,有
、在7个位置中任取4个,安排除甲、乙、丙之外的4人,有![]() 种排法,
种排法,
![]() 、将甲、乙、丙按从左到右的顺序安排在剩余的3个空位中,只有1种排法,
、将甲、乙、丙按从左到右的顺序安排在剩余的3个空位中,只有1种排法,
则甲、乙、丙按从左到右的顺序排列的排法有![]() 种.
种.


科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
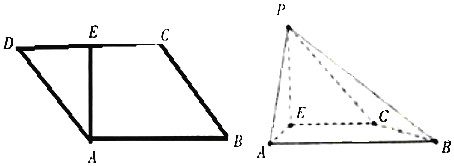
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在![]() 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为﹣1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2<ex;
(3)证明:对任意给定的正数c,总存在x0 , 使得当x∈(x0 , +∞)时,恒有x2<cex .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一中最强大脑社对高中学生的记忆力![]() 和判断力
和判断力![]() 进行统计分析,得下表数据
进行统计分析,得下表数据

参考公式: ,
,![]() .
.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,预测记忆力为
,预测记忆力为![]() 的同学的判断力.
的同学的判断力.
(2)若记忆力增加![]() 个单位,预测判断力增加多少个单位?
个单位,预测判断力增加多少个单位?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位数学老师在黑板上写了三个向量![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 都是给定的整数.老师问三位学生这三个向量的关系,甲回答:“
都是给定的整数.老师问三位学生这三个向量的关系,甲回答:“![]() 与
与![]() 平行,且
平行,且![]() 与
与![]() 垂直”,乙回答:“
垂直”,乙回答:“![]() 与
与![]() 平行”,丙回答:“
平行”,丙回答:“![]() 与
与![]() 不垂直也不平行”,最后老师发现只有一位学生判断正确,由此猜测
不垂直也不平行”,最后老师发现只有一位学生判断正确,由此猜测![]() ,
,![]() 的值不可能为( )
的值不可能为( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(4cos2(
=(4cos2(![]() -
-![]() ),cosx+sinx),
),cosx+sinx),![]() =(sinx,cosx-sinx),设f(x)=
=(sinx,cosx-sinx),设f(x)=![]()
![]() -1
-1
(1)求满足|f(x)|≤1的实数x的集合;
(2)若函数φ(x)=![]() [f(2x)+tf(x)-tf(
[f(2x)+tf(x)-tf(![]() -x)]-(1+
-x)]-(1+![]() )在[-
)在[-![]() ,
,![]() ]上的最大值为2,求实数t的值.
]上的最大值为2,求实数t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com