
设![]() 为等比数列,
为等比数列,![]() 为等差数列,且
为等差数列,且![]() ,
,![]() ,若数列
,若数列![]() 是1,1,2,…,则数列
是1,1,2,…,则数列![]() 的前10项之和为( )
的前10项之和为( )
A.978 B.557 C.476 D.以上答案都不对
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三第一学期期中考试理科数学试卷(解析版) 题型:解答题
设等比数列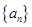 的首项为
的首项为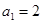 ,公比为
,公比为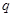 (
(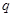 为正整数),且满足
为正整数),且满足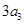 是
是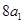 与
与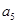 的等差中项;数列
的等差中项;数列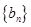 满足
满足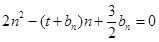 (
(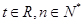 ).
).
(1)求数列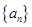 的通项公式;
的通项公式;
(2)试确定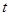 的值,使得数列
的值,使得数列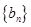 为等差数列;
为等差数列;
(3)当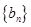 为等差数列时,对每个正整数
为等差数列时,对每个正整数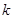 ,在
,在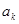 与
与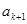 之间插入
之间插入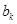 个2,得到一个新数列
个2,得到一个新数列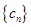 . 设
. 设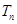 是数列
是数列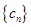 的前
的前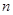 项和,试求满足
项和,试求满足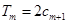 的所有正整数
的所有正整数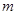 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三第一学期期中考试文科数学试卷(解析版) 题型:解答题
设等比数列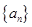 的首项为
的首项为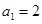 ,公比为
,公比为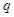 (
(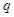 为正整数),且满足
为正整数),且满足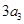 是
是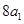 与
与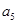 的等差中项;数列
的等差中项;数列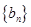 满足
满足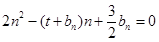 (
(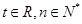 ).
).
(Ⅰ)求数列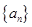 的通项公式;
的通项公式;
(Ⅱ)试确定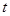 的值,使得数列
的值,使得数列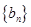 为等差数列;
为等差数列;
(Ⅲ)当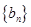 为等差数列时,对每个正整数
为等差数列时,对每个正整数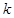 ,在
,在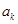 与
与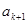 之间插入
之间插入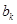 个2,得到一个新数列
个2,得到一个新数列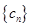 . 设
. 设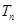 是数列
是数列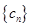 的前
的前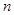 项和,试求满足
项和,试求满足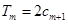 的所有正整数
的所有正整数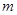 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市徐汇区高三第一学期期中试卷数学 题型:解答题
(1)等比数列 中,对任意
中,对任意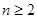 ,
, 时都有
时都有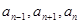 成等差,求公比
成等差,求公比 的值
的值
(2)设 是等比数列
是等比数列 的前
的前 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由
(3)设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 与
与 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源:湖南省长沙市一中2010届高三第一次模拟考试(理) 题型:解答题
已知等比数列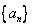 的首项为
的首项为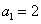 ,公比为
,公比为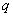 (
(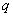 为正整数),且满足
为正整数),且满足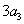 是
是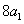 与
与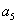 的等差中项;数列
的等差中项;数列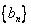 满足
满足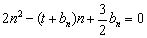 (
(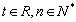 ).
).
(1)求数列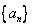 的通项公式;
的通项公式;
(2)试确定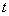 的值,使得数列
的值,使得数列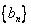 为等差数列;
为等差数列;
(3)当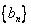 为等差数列时,对任意正整数
为等差数列时,对任意正整数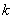 ,在
,在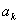 与
与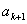 之间插入2共
之间插入2共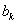 个,得到一个新数列
个,得到一个新数列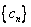 .设
.设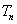 是数列
是数列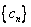 的前
的前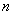 项和,试求满足
项和,试求满足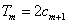 的所有正整数
的所有正整数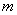 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com