
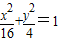 上有两点P,Q,O是坐标原点,若OP,OQ的斜率之积为-
上有两点P,Q,O是坐标原点,若OP,OQ的斜率之积为- .
. ,可得α-β=2kπ±
,可得α-β=2kπ±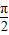 ,进而可得|OP|2+|OQ|2是定值;
,进而可得|OP|2+|OQ|2是定值; ,
,
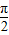 ,k∈Z.
,k∈Z. =cosα+cosβ①,y=sinα+sinβ②
=cosα+cosβ①,y=sinα+sinβ② =2,即
=2,即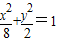 .
.

科目:高中数学 来源: 题型:
 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且| AC |
| BC |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| PQ |
| AC |
查看答案和解析>>
科目:高中数学 来源:2013届山东省临沂市高二上学期期末质量检测调研文科数学 题型:选择题
椭圆 上有两点P、Q ,O为原点,若OP、OQ斜率之积为
上有两点P、Q ,O为原点,若OP、OQ斜率之积为
则 为
为
A . 4 B. 20 C. 64 D. 不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com