
 的右焦点,第一象限内的点M在椭圆上,若MF⊥x轴,直线MN与圆x2+y2=1相切于第四象限内的点N,则|NF|等于( )
的右焦点,第一象限内的点M在椭圆上,若MF⊥x轴,直线MN与圆x2+y2=1相切于第四象限内的点N,则|NF|等于( )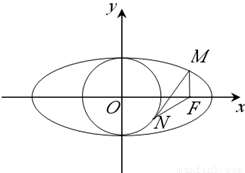
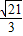
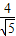
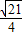
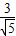
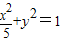 的右焦点,
的右焦点,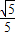 )
)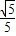 =k(x-2)
=k(x-2)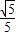 =0
=0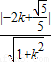 =1
=1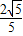 ,或k=
,或k=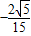 (舍去)
(舍去)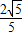 x-y-
x-y-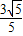 =0…①
=0…① ,
, )
)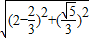 =
=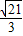


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高二上学期质量检测数学理卷 题型:选择题
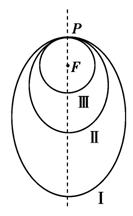
如右图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月
球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞
行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ
绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ
绕月飞行,若用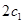 和
和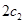 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用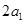 和
和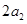
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①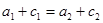 ②
②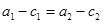 ③
③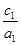 <
<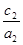 ④
④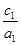 >
>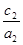 .
.
其中正确式子的序号是 ( )
(A)①③ (B)②③ (C)①④ (D)②④
 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市十三校高三(下)第二次联考数学试卷(理科)(解析版) 题型:解答题
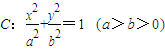 的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为
的左、右顶点分别为A、B,椭圆C的右焦点为F,过F作一条垂直于x轴的直线与椭圆相交于R、S,若线段RS的长为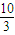 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com