
【题目】已知函数![]() ,
, ![]() R.
R.
(1)证明:当![]() 时,函数
时,函数![]() 是减函数;
是减函数;
(2)根据![]() 的不同取值,讨论函数
的不同取值,讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)当![]() ,且
,且![]() 时,证明:对任意
时,证明:对任意![]() ,存在唯一的
,存在唯一的![]() R,使得
R,使得![]() ,且
,且![]() .
.
【答案】(1)见解析(2) 当![]() 时,函数
时,函数![]() 是奇函数;当
是奇函数;当![]() 时,函数
时,函数![]() 是偶函数;当
是偶函数;当![]() 且
且![]() 时,函数
时,函数![]() 是非奇非偶函数,(3)见解析
是非奇非偶函数,(3)见解析
【解析】试题分析:
(1)任取![]() ,设
,设![]() ,计算可得
,计算可得 ,据此可得
,据此可得![]() ,函数
,函数![]() 是减函数.
是减函数.
(2)分类讨论可得:当![]() 时,函数
时,函数![]() 是偶函数,当
是偶函数,当![]() 时函数
时函数![]() 是奇函数,当
是奇函数,当![]() 且
且![]() 时,函数
时,函数![]() 是非奇非偶函数.
是非奇非偶函数.
(3)由(1)知,当![]() 时函数
时函数![]() 是减函数,结合函数的单调性分别证明
是减函数,结合函数的单调性分别证明![]() 的存在性(利用函数的值域)和唯一性(利用反证法)即可证得题中的结论.
的存在性(利用函数的值域)和唯一性(利用反证法)即可证得题中的结论.
试题解析:
(1)任取![]() ,设
,设![]() ,则
,则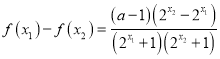 ,
,
∵![]() ,所以
,所以![]() ,又
,又![]() ,∴
,∴![]() ,即
,即![]() ,
,
所以当![]() 时,函数
时,函数![]() 是减函数.
是减函数.
(2)当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 是偶函数,
是偶函数,
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以函数![]() 是奇函数,
是奇函数,
当![]() 且
且![]() 时,
时, ![]() ,
, ![]() ,
,
因为![]() 且
且![]() ,
,
所以函数![]() 是非奇非偶函数.
是非奇非偶函数.
(3)由(1)知,当![]() 时函数
时函数![]() 是减函数,
是减函数,
所以函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
因为![]() ,所以存在
,所以存在![]() ,使得
,使得![]() .
.
假设存在![]() 使得
使得![]() ,
,
若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() ,
,
与![]() 矛盾,故
矛盾,故![]() 是唯一的,
是唯一的,
假设![]() ,即
,即![]() 或
或![]() ,则
,则![]() 或
或![]() ,
,
所以![]() ,与
,与![]() 矛盾,故
矛盾,故![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】自治区有甲、乙两位航模运动员参加了国家队集训,现分别从他们在集训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(I)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩中的位数;
(II)现要从中派一人参加国际比赛,从平均成绩和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为F1,F2,点P 在椭圆上运动,
的左右焦点分别为F1,F2,点P 在椭圆上运动, ![]() 的最大值为m,
的最大值为m, ![]() 的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,AB=BC,D、E分别为
中,AB=BC,D、E分别为![]() 的中点.
的中点.

(1)证明:ED为异面直线BB1与AC1的公垂线段;
(2)设AB=1, ![]() ,求二面角A1—AD—C1的大小.
,求二面角A1—AD—C1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
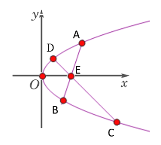
【题目】已知点![]() 为抛物线
为抛物线![]() 内一定点,过
内一定点,过![]() 作两条直线交抛物线于
作两条直线交抛物线于![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点.
的中点.
(1)当![]() 时,求△
时,求△![]() 的面积的最小值;
的面积的最小值;
(2)若![]() 且
且![]() ,证明:直线
,证明:直线![]() 过定点,并求定点坐标。
过定点,并求定点坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com