分析:(I)连接A1B,交AB1于O点,连接OD,由平行四边形性质及三角形中位线定理可得OD∥BC1,进而由线面平行的判定定理得到BC1∥平面AB1D;
(II)由直棱柱的几何特征可得A1A⊥B1D,由等边三角形三线合一可得B1D⊥A1C1,进而由线面垂直的判定定理得到B1D⊥平面AA1C1C,再由三角形相似得到A1C⊥AD后,可证得A1C⊥平面AB1D.
(III)由(I)中OD∥BC1,可得异面直线AD与BC1所成角即∠ADO,解△ADO可得答案.
解答: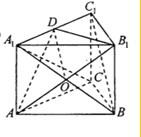
证明:(I)在三棱柱ABC-A
1B
1C
1中,连接A
1B,交AB
1于O点,连接OD
∵在△A
1BC
1中,A
1D=DC
1,A
1O=OB,
∴OD∥BC
1,
又∵OD?平面AB
1D,BC
1?平面AB
1D;
∴BC
1∥平面AB
1D;
(II)在三棱柱ABC-A
1B
1C
1中,A
1A⊥平面A
1B
1C
1;
∵B
1D?平面A
1B
1C
1;
∴A
1A⊥B
1D
在△A
1B
1C
1中,D为A
1C
1的中点
∴B
1D⊥A
1C
1又∵A
1A∩A
1C
1=A
1,A
1A,A
1C
1?平面AA
1C
1C,
∴B
1D⊥平面AA
1C
1C,
又∵A
1C?平面AA
1C
1C,
∴B
1D⊥A
1C
又∵
=
=
∴∠DA
1A=∠A
1AC=90°
∴△DA
1A∽△A
1AC,∠ADA
1=∠CA
1A
∵∠DA
1C+∠CA
1A=90°
∴∠DA
1C+∠ADA
1=90°
∴A
1C⊥AD
又∵B
1D∩AD=D,B
1D,AD?平面AB
1D;
∴A
1C⊥平面AB
1D;
解:(III)由(I)得,OD∥BC
1,
故AD与BC
1所成的角即为∠ADO
在△ADO中,AD=
,OD=
BC
1=
,AO=
A
1B=
,
∵AD
2=OD
2+AO
2,OD=AO
∴△ADO为等腰直角三角形
故∠ADO=45°
即异面直线AD与BC
1所成角等于45°
点评:本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,直线与平面平行的判定,(I)的关键是证得OD∥BC1,(II)的关键是熟练掌握线面垂直与线线垂直之间的转化,(III)的关键是得到异面直线AD与BC1所成角即∠ADO.

 (2013•和平区二模)如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=
(2013•和平区二模)如图,正三棱柱ABC-A1B1C1中,AB=2,AA1= 证明:(I)在三棱柱ABC-A1B1C1中,连接A1B,交AB1于O点,连接OD
证明:(I)在三棱柱ABC-A1B1C1中,连接A1B,交AB1于O点,连接OD

 阅读快车系列答案
阅读快车系列答案