
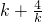 与4的大小即可得到原不等式的解集;当k等于2时,代入不等式,根据完全平方式大于0,得到x不等于4,进而得到原不等式的解集;当k小于0时,不等式两边都除以k把不等式变形后,根据
与4的大小即可得到原不等式的解集;当k等于2时,代入不等式,根据完全平方式大于0,得到x不等于4,进而得到原不等式的解集;当k小于0时,不等式两边都除以k把不等式变形后,根据 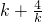 小于4,得到原不等式的解集,综上,得到原不等式的解集;
小于4,得到原不等式的解集,综上,得到原不等式的解集;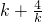 )](x-4)>0,
)](x-4)>0,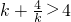 ,
,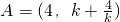 ,要使不存在整数x使不等式(kx-k2-4)(x-4)<0成立,
,要使不存在整数x使不等式(kx-k2-4)(x-4)<0成立,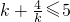 ,解得:1≤k≤4;
,解得:1≤k≤4;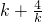 )](x-4)>0,
)](x-4)>0,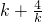 )∪(4,+∞),不合题意,
)∪(4,+∞),不合题意,

 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
|
| f(n)•f(n+1) |
| 2n |
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州高级中学高一(上)期末数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com