
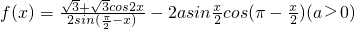 的最大值为2.
的最大值为2.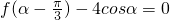 ,求
,求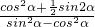 的值.
的值.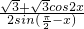 -2asin
-2asin cos(π-
cos(π- )
) +asinx…3分
+asinx…3分 cosx+asinx(x≠kπ+
cosx+asinx(x≠kπ+ ,k∈Z)…4分
,k∈Z)…4分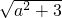 sin(x+φ)(其中tanφ=
sin(x+φ)(其中tanφ=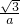 ),…5分
),…5分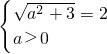 ,解得a=2…7分
,解得a=2…7分 ),
), )-4cosα=0,
)-4cosα=0,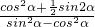
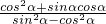

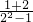
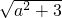 sin(x+φ)(其中tanφ=
sin(x+φ)(其中tanφ=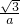 ),依题意列方程即可求得a的值;
),依题意列方程即可求得a的值; ),结合条件f(α-
),结合条件f(α- )-4cosα=0可求得tanα的值,从而可求
)-4cosα=0可求得tanα的值,从而可求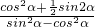 的值.
的值. )是关键,属于中档题.
)是关键,属于中档题. 

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com