���𰸡�
��������1������f��x���ĵ������䡱���������κ������ԣ����õ������������ö���ĸa�������ۣ�
��2�����������⣬��Ϲ۲�f��x����ͼ�����������⣮
����⣺��1�������⣬��f�䣨x��=x
2+2ax+b��
��f�䣨-1��=1-2a+b=0��b=2a-1
�Ӷ�f��x��=

x
3+ax
2+��2a-1��x��
��f�䣨x��=��x+1����x+2a-1��
��f�䣨x��=0����x=-1��x=1-2a
�ٵ�a��1ʱ��1-2a��-1
��x�仯ʱ������f�䣨x����f��x���ı仯����ã�
����f��x���ĵ���������Ϊ��-�ޣ�1-2a���ͣ�-1��+�ޣ�������������Ϊ��1-2a��-1��
�ڵ�a=1ʱ��1-2a=-1����ʱ��f�䣨x����0��������ҽ���x=-1��f�䣨x��=0���ʺ���f��x���ĵ���������ΪR��
�۵�a��1ʱ��1-2a��-1��ͬ���ɵã�����f��x���ĵ���������Ϊ��-�ޣ�-1���ͣ�1-2a��+�ޣ���
������������-1��1-2a��
���ϣ���a��1ʱ������f��x���ĵ���������Ϊ��-�ޣ�1-2a���ͣ�-1��+�ޣ�������������Ϊ��1-2a��-1����
��a=1ʱ������f��x���ĵ���������ΪR��
��a��1ʱ������f��x���ĵ���������Ϊ��-�ޣ�-1���ͣ�1-2a��+�ޣ�������������Ϊ��-1��1-2a��
��2��������a=-1��f��x��=

x
3-x
2-3x
��f�䣨x��=x
2-2x-3=0��x
1=-1��x
2=3
�ɣ�1����f��x��������Ϊ��-�ޣ�-1���ͣ�3��+�ޣ�������������Ϊ��-1��3����
���Ժ���f��x���ڴ�x
1=-1��x
2=3��ȡ�ü�ֵ����M��-1��

����N��3��-9��
�۲�f��x����ͼ������������

�ٵ�m��-1������-1���仯��3ʱ���߶�MP��б��������f��x���ڵ�P�����ߵ�б��f��x��֮��Kmp-f�䣨m����ֵ����������Ϊ����
���߶�MP�������Ƿ�������H��P�Ĺ�������Kmp-f�䣨m����m�����������еĹ�����
��Kmp-f�䣨m��=0��Ӧ��λ�ÿ������ٽ�㣬���Ʋ⣺����Kmp-f�䣨m����m���������t��Сֵ���������֤����ȷ����t��Сֵ������f��x���ڵ�P��m��f��m������������б��f�䣨m��=m
2-2m-3��
�߶�MP��б��Kmp=
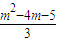
��
��Kmp-f�䣨m��=0ʱ�����m=-1��m=2��
ֱ��MP�ķ���Ϊy=��
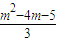
x+
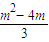
����
��g��x��=f��x��-��

x+
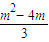
����
��m=2ʱ��g�䣨x��=x
2-2x�ڣ�-1��2����ֻ��һ�����x=0�����ж�f��x�������ڣ�-1��0���ϵ����������ڣ�0��2���ϵ����ݼ�����g��-1��=g��2��=0������g��x���ڣ�-1��2����û����㣬���߶�MP������f��x��û������M��P�Ĺ����㡢
��m�ʣ�2��3]ʱ��g��0��=-
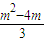
��0��
g��2��=-��m-2��
2��0��
���Դ��ڦġʣ�0��2]ʹ��g���ģ�=0��
����m�ʣ�2��3]ʱ��MP������f��x��������M��P�Ĺ�����
���ϣ�t����СֵΪ2��
�������ƣ�1�����еĹ۲죬�ɵ�m��ȡֵ��ΧΪ��1��3]��
�����������ۺϿ����˺����������ۺ�Ӧ�ã������Ǻ������ۺ��⣬�ۺϿ��������õ��������ĵ������䣬�����ļ�ֵ���Լ����������⣬��һ�����Ѷȣ���һ���ܺõ�ѹ���⣮

 x3+ax2+bx����f�䣨-1��=0��
x3+ax2+bx����f�䣨-1��=0�� x3+ax2+��2a-1��x��
x3+ax2+��2a-1��x�� x3-x2-3x
x3-x2-3x ����N��3��-9��
����N��3��-9��
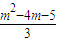 ��
��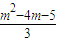 x+
x+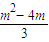 ����
���� x+
x+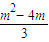 ����
����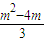 ��0��
��0��


 ��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��
��֪����f��x��=Asin����x+�գ���x��R��A��0���أ�0��|��|��