
【题目】设函数![]() .
.
![]() 求函数
求函数![]() 的单调区间和极值.
的单调区间和极值.
![]() 若函数
若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围.
内恰有两个零点,求a的取值范围.
【答案】(1)见解析; (2)![]()
【解析】
![]() 求出函数的导数,通过讨论a的范围,求出函数的单调区间和极值即可;
求出函数的导数,通过讨论a的范围,求出函数的单调区间和极值即可;
![]() 通过讨论a的范围,若满足
通过讨论a的范围,若满足![]() 在区间
在区间![]() 内恰有两个零点,需满足
内恰有两个零点,需满足 ,解出即可.
,解出即可.
![]() 由
由![]() ,得
,得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,函数无极大值,也无极小值;
上单调递增,函数无极大值,也无极小值;
![]() 当
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() 舍去
舍去![]() .
.
于是,当x变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
x |
|
|
|
|
| 0 |
|
| 递减 |
| 递增 |
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
综上可知,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,函数既无极大值也无极小值;
,函数既无极大值也无极小值;
当![]() 时,函数
时,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间为
,单调递增区间为![]() ,
,
函数![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
![]() 当
当![]() 时,由
时,由![]() 知函数
知函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故函数![]() 在区间
在区间![]() 上至多有一个零点,不合题意.
上至多有一个零点,不合题意.
当![]() 时,由
时,由![]() 知,当
知,当![]() 时,函数
时,函数![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
所以函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
若函数![]() 在区间
在区间![]() 内恰有两个零点,
内恰有两个零点,
则需满足 ,即
,即 整理得
整理得 ,所以
,所以![]() .
.
故所求a的取值范围为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题正确的是( )
①线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合的效果越好;
越小,说明模型的拟合的效果越好;
④随机误差![]() 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足![]() .
.
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为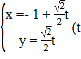 为参数
为参数![]() .
.
![]() 若
若![]() ,直线l与x轴的交点为M,N是圆C上一动点,求
,直线l与x轴的交点为M,N是圆C上一动点,求![]() 的最小值;
的最小值;
![]() 若直线l被圆C截得的弦长等于圆C的半径,求a的值.
若直线l被圆C截得的弦长等于圆C的半径,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a<2,函数f(x)=(x2+ax+a)ex.
(1)当a=1时,求f(x)的单调递增区间;
(2)若f(x)的极大值是6e-2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足:a1=![]() ,a2=
,a2=![]() ,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则
,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则![]() 的值为( )
的值为( )
A. 5032 B. 5044 C. 5048 D. 5050
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月5日上午,首届中国国际进口博览会拉开大幕,这是中国也是世界上首次以进口为主题的国家级博览会,本次博览会包括企业产品展、国家贸易投资展,其中企业产品展分为7个展区,每个展区统计了备受关注百分比,如下表:
展区类型 | 智能及高端装备 | 消费电子及家电 | 汽车 | 服装服饰及日用消费品 | 食品及农产品 | 医疗器械及医药保健 | 服务贸易 |
展区的企业数 | 400 | 60 | 70 | 650 | 1670 | 300 | 450 |
备受关注百分比 |
|
|
|
|
|
|
|
备受关注百分比指:一个展区中受到所有相关人士关注![]() 简称备受关注
简称备受关注![]() 的企业数与该展区的企业数的比值.
的企业数与该展区的企业数的比值.
(1)从企业产品展7个展区的企业中随机选取1家,求这家企业是选自“智能及高端装备”展区备受关注的企业的概率;
(2)某电视台采用分层抽样的方法,在“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中抽取6家进行了采访,若从受访企业中随机抽取2家进行产品展示,求恰有1家来自于“医疗器械及医药保健”展区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,顶点为原点的抛物线![]() ,它是焦点为椭圆
,它是焦点为椭圆![]() 的右焦点.
的右焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过抛物线![]() 的焦点作互相垂直的两条直线分别交抛物线
的焦点作互相垂直的两条直线分别交抛物线![]() 于
于![]() 四点,求四边形
四点,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com