解:(1)在△PAB中,由余弦定理,有2
2=a
2+b
2-2abcosC,

,
所以,点P的轨迹C是以A,B为焦点,长轴长
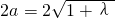
的椭圆.(除去长轴上的顶点)
如图,以A、B所在的直线为x轴,以A、B的中点为坐标原点建立直角坐标系.
则,A(-1,0)和B(1,0).
椭圆C的标准方程为:

(y≠0).
(2)设M(x
1,y
1),N(x
2,y
2),
①当MN垂直于x轴时,MN的方程为x=1,由题意,有M(1,1),N(1,-1)在椭圆上.
即

,由λ>0,得

.
②当MN不垂直于x轴时,设MN的方程为y=k(x-1).
由

得:[λ+(1+λ)k
2]x
2-2(1+λ)k
2x+(1+λ)(k
2-λ)=0,
由题意知:λ+(1+λ)k
2>0,
所以

,

.
于是:

.
因为OM⊥ON,所以

,
所以

,
所以,

,
由λ>0得1+λ-λ
2>0,解得

.
综合①②得:

.
分析:(1)在△PAB中,由余弦定理,有2
2=a
2+b
2-2abcosC,

,故点P的轨迹C是以A,B为焦点,长轴长
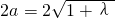
的椭圆,由此能求出椭圆C的方程.
(2)设M(x
1,y
1),N(x
2,y
2),当MN垂直于x轴时,MN的方程为x=1,由题意,

,由λ>0,得

.当MN不垂直于x轴时,设MN的方程为y=k(x-1).由

得:[λ+(1+λ)k
2]x
2-2(1+λ)k
2x+(1+λ)(k
2-λ)=0,由题意知:λ+(1+λ)k
2>0,再由韦达定理能导出

.由此可知

.
点评:本题考动点C的轨迹方程和确定λ的范围.解题时要认真审题,仔细解答,注意韦达定理和椭圆性质的应用.

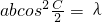 .
. ,
,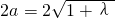 的椭圆.(除去长轴上的顶点)
的椭圆.(除去长轴上的顶点) (y≠0).
(y≠0). ,由λ>0,得
,由λ>0,得 .
. 得:[λ+(1+λ)k2]x2-2(1+λ)k2x+(1+λ)(k2-λ)=0,
得:[λ+(1+λ)k2]x2-2(1+λ)k2x+(1+λ)(k2-λ)=0, ,
, .
. .
. ,
, ,
, ,
, .
. .
. ,故点P的轨迹C是以A,B为焦点,长轴长
,故点P的轨迹C是以A,B为焦点,长轴长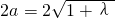 的椭圆,由此能求出椭圆C的方程.
的椭圆,由此能求出椭圆C的方程. ,由λ>0,得
,由λ>0,得 .当MN不垂直于x轴时,设MN的方程为y=k(x-1).由
.当MN不垂直于x轴时,设MN的方程为y=k(x-1).由 得:[λ+(1+λ)k2]x2-2(1+λ)k2x+(1+λ)(k2-λ)=0,由题意知:λ+(1+λ)k2>0,再由韦达定理能导出
得:[λ+(1+λ)k2]x2-2(1+λ)k2x+(1+λ)(k2-λ)=0,由题意知:λ+(1+λ)k2>0,再由韦达定理能导出 .由此可知
.由此可知 .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案