
从某校高二年级 名男生中随机抽取
名男生中随机抽取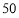 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在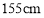 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组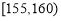 ,第二组
,第二组 , ,第八组
, ,第八组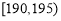 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
分组 | 频数 | 频率 | 频率/组距 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
频率分布直方图如下:

(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取 名男生,记他们的身高分别为
名男生,记他们的身高分别为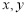 ,求满足:
,求满足: 的事件的概率.
的事件的概率.
(1)详见解析;(2) .
.
【解析】
试题分析:(1)由频率和为1,及题设条件得出样本中6、7组的人数为7人,由已知:x+m=7,x,m,2成等差数列,故可求得答案.
(2) 从身高属于第6组和第8组的所有男生中随机的抽取2名男生,记他们的身高分别为x、y,求满足:|x-y|≤5事件的概率,这是一个古典概率模型的问题.用列举法列出基本事件的个数与事件工包含的基本事件数,用古典概率模型的公式求概率..
试题解析:(1) 由频率分布直方图得前五组的频率是
 ,
,
第 组的频率是
组的频率是 ,所以第
,所以第 组的频率是
组的频率是 ,所以样本中第
,所以样本中第 组的总人数为
组的总人数为 人.由已知得:
人.由已知得:  ①
①
 成等差数列,
成等差数列, ②
②
由①②得: ,所以
,所以 4分
4分
频率分布直方图如下图所示:
 6分
6分
(2)由(1)知,身高在 内的有
内的有 人,设为
人,设为 ,身高在
,身高在 内的有
内的有 人,设为
人,设为
若 ,则有
,则有 共
共 种情况;
种情况;
若 ,则有
,则有 共
共 种情况;
种情况;
若 ,
, 或
或 ,
, ,则有
,则有
 共
共 种情况
种情况
∴基本事件总数为 ,而事件 “
,而事件 “ ”所包含的基本事件数为
”所包含的基本事件数为 ,故
,故 . 14分
. 14分
考点:1.频率分布直方图;2.等可能事件的概率..


科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考理科数学试卷(解析版) 题型:选择题
已知 是双曲线
是双曲线 上不同的三点,且
上不同的三点,且 连线经过坐标原点,若直线
连线经过坐标原点,若直线 的斜率乘积
的斜率乘积 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届湖北部分重点中学高二上学期期末考试理科数学试卷(解析版) 题型:选择题
如果方程 表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )
表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )
A. B.
B.
C. D.
D.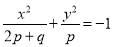
查看答案和解析>>
科目:高中数学 来源:2015届湖北部分重点中学高二上学期期末考试文科数学试卷(解析版) 题型:填空题
若命题p:?x ,y∈R,x2+y2-1>0,则该命题p的否定是__________.
查看答案和解析>>
科目:高中数学 来源:2015届湖北部分重点中学高二上学期期末考试文科数学试卷(解析版) 题型:选择题
在研究打酣与患心脏病之间的关系中,通过收集数据、整理分析数据得“打酣与患心脏病有关”的结论,并且有 以上的把握认为这个结论是成立的。下列说法中正确的是( )
以上的把握认为这个结论是成立的。下列说法中正确的是( )
A.100个心脏病患者中至少有99人打酣
B.1个人患心脏病,那么这个人有99%的概率打酣
C.在100个心脏病患者中一定有打酣的人
D.在100个心脏病患者中可能一个打酣的人都没有
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:填空题
欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.已知铜钱是直径为4cm的圆面,中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴整体不出边界),则油滴整体(油滴是直径为0.2cm的球)正好落入孔中的概率是 (不作近似计算) .
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:选择题
甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为
 ,中位数分别为
,中位数分别为 ,
, ,则
,则

A.  <
< ,
, >
> B.
B.  <
< ,
, 


C.  >
> ,
,  >
> D.
D.  >
> ,
,  <
<
查看答案和解析>>
科目:高中数学 来源:2015届湖北孝感高级中学高二上学期期末考试文科数学试卷(解析版) 题型:填空题
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,若它落在阴影区域内的概率为 ,则阴影区域的面积为 .
,则阴影区域的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com