
(本小题满分14分)如图,在长方体 中,
中, ,
, ,点
,点 在棱
在棱 上移动.
上移动.

⑴ 证明: //平面
//平面 ;
;
⑵ 证明: ⊥
⊥ ;
;
⑶ 当 为
为 的中点时,求四棱锥
的中点时,求四棱锥 的体积.
的体积.
(1)证明:见解析;(2) 证明:见解析;(3) E-ACD1的体积为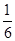 .
.
【解析】
试题分析:(1)利用线线平行的来证明线面平行。
(2)由AE⊥平面AA1DD1,A1D⊂平面AA1DD1,知A1D⊥AE,再由AA1DD1为正方形,利用直线与平面垂直的性质,能够证明A1D⊥D1E.
(3) 设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=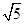 ,AD1=
,AD1=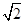 ,先求出△AD1C和△ACE的面积,再求出三棱锥D1-AEC的体积,由此能够求出点E到面ACD1的距离.进而得到体积。
,先求出△AD1C和△ACE的面积,再求出三棱锥D1-AEC的体积,由此能够求出点E到面ACD1的距离.进而得到体积。
(1)证明:∵ ABCD-A1B1C1D1是长方体
∴AB// D1C1,AB=D1C1, ……1分
∴AB C1 D1为平行四边形,……2分
∴B C1 // AD1, ……3分
又B C1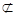 平面ACD1,AD1Ì平面ACD1, ……4分
平面ACD1,AD1Ì平面ACD1, ……4分
所以BC1//平面ACD1. ……5分
(2) 证明:∵ AE⊥平面AA1D1D,A1DÌ平面AA1D1D,
∴ A1D⊥AE, ……6分
AA1D1D为正方形,∴A1D⊥A D1 , ……7分
又A1D∩AE =A,∴A1D⊥平面AD1E, ……9分
A1DÌ平面AD1E,∴A1D⊥D1E, ……10分
(3) 解: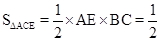 , ……12分
, ……12分
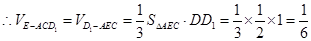 ……13分
……13分
所以E-ACD1的体积为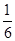 .
……14分
.
……14分
考点:本试题主要考查了空间中点线面的位置关系的运用证明线线的垂直,和线面平行以及几何体的体积的综合运用。
点评:解决该试题的关键是对于线面平行的判定定理和线面垂直的性质定理的灵活运用和熟练掌握,同时对于体积的求解,一般就是研究几何体的高既可以得到。


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 天的销售量为
天的销售量为 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额 关于第
关于第 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
⑴ 求 ,
, 满足的关系式;
满足的关系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
⑶ 证明: (
( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com