练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知

    （1）若p >1时，解关于x的不等式；

    （2）若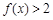对时恒成立，求p的范围.

     

    【答案】

    (1) ①，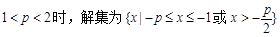

    ② p = 2时，解集为，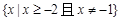

    ③ p > 2时，解集为；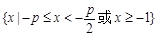 

    (2) p > 2

    【解析】

    试题分析：（1）先因式分解把原不等式转化为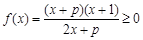．再对三个根的大小进行讨论求解.

    （2）解本小题的关键是把,，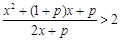

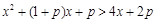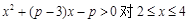    ∴ 恒成立，最终转化为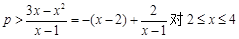恒成立来解决，然后再构造函数求最值即可.

    (1) 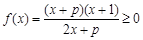·························· 1分

    ①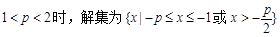················· 3分

    ② p = 2时，解集为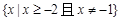····················· 5分

    ③ p > 2时，解集为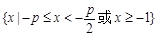·················· 7分

    (2)

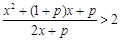
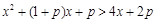    ··························· 8分

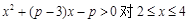    ∴ 恒成立

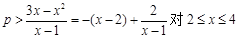    ∴ 恒成立················· 9分

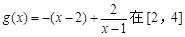    ∵ 上递减···················· 10分

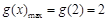    ∴ ····························· 11分

    ∴ p > 2    12分

    考点：解式不等式的解法，不等式恒成立，函数的最值.

    点评：（1）分式不等式求解时一般要用数轴穿根法求解.（2）不等式恒成立问题一般要注意参数与变量分离，然后转化为函数最值来研究.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知

    （1）若p > 1时，解关于x的不等式；

    （2）若对时恒成立，求p的范围．

    查看答案和解析>>

    科目：高中数学 来源：西南师大附中2010届高三第五次月考（数学理）试题 题型：解答题

    已知

    （1）若p > 1时，解关于x的不等式；

    （2）若对时恒成立，求p的范围．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知数学公式
    （1）若p＞1时，解关于x的不等式f（x）≥0；
    （2）若f（x）＞2对2≤x≤4时恒成立，求p的范围．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年重庆市西南师大附中高三（上）1月月考数学试卷（文科）（解析版） 题型：解答题

    已知
    （1）若p＞1时，解关于x的不等式f（x）≥0；
    （2）若f（x）＞2对2≤x≤4时恒成立，求p的范围．

    查看答案和解析>>

    同步练习册答案