
|
(I)x-![]() y+1=0,或x+
y+1=0,或x+![]() y+1=0 (Ⅱ)
y+1=0 (Ⅱ)![]()
(解 (1)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0.…2 分 设A(x1,y1),B(x2,y2),
|
 4分由线段AB中点的横坐标是-
4分由线段AB中点的横坐标是-(2)假设在x轴上存在点M(m,0),使![]() 为常数.
为常数.
(ⅰ)当直线AB与x轴不垂直时,由(1)知x1+x2=-![]() ,x1x2=
,x1x2=![]() . ③
. ③
所以![]() =(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1+1)(x2+1)=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2.
=(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1+1)(x2+1)=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2.
将③代入,整理得![]() =
=![]() +m2=
+m2=![]() +m2=m2+2m-
+m2=m2+2m-![]() -
-![]() . 11分注意到
. 11分注意到![]() 是与k无关的常数,从而有6m+14=0,m=-
是与k无关的常数,从而有6m+14=0,m=-![]() ,此时
,此时![]() =
=![]() .…12分
.…12分
(ⅱ)当直线AB与x轴垂直时,此时点A,B的坐标分别为![]() 、
、![]() ,
,
当m=-![]() 时,亦有
时,亦有![]() =
=![]() .综上,在x轴上存在定点M
.综上,在x轴上存在定点M![]() ,使
,使![]() 为常数. 14分
为常数. 14分


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
|
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)设bn=
的通项公式;(Ⅱ)设bn=![]() ,Tn是数列{bn}的前n项和,求
,Tn是数列{bn}的前n项和,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
(Ⅰ)求这3个数中,恰有一个是偶数的概率;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)记ξ为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时ξ的值是2)。求随机变量ξ的分布列及其数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
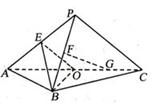
(I)设![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(II)证明:在![]() 内存在一点
内存在一点![]() ,使
,使![]() 平面
平面![]() ,并求点
,并求点![]() 到
到![]() ,
,![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
其中![]() .
.
(I)设函数![]() .若
.若![]() 在区间
在区间![]() 上不单调,求
上不单调,求![]() 的取值范围;
的取值范围;
(II)设函数![]() 是否存在
是否存在![]() ,对任意给定的非零实数
,对任意给定的非零实数![]() ,存在惟一
,存在惟一
的非零实数![]() (
(![]() ),使得
),使得![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存
的值;若不存
在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com