
(04年天津卷理)(12分)
如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,E是PC的中点,作
,E是PC的中点,作![]() 交PB于点F。
交PB于点F。
(I)证明 ![]() 平面
平面![]() ;
;
(II)证明![]() 平面EFD;
平面EFD;
(III)求二面角![]() 的大小。
的大小。
|
解析:方法一:
(I) 证明:连结AC,AC交BD于O。连结EO。
|
![]() 底面ABCD是正方形,
底面ABCD是正方形,![]() 点O是AC的中点
点O是AC的中点
在![]() 中,EO是中位线,
中,EO是中位线,![]() 。
。
而![]() 平面EDB且
平面EDB且![]() 平面EDB,
平面EDB,
所以,![]() 平面EDB。 。。。。。。。。。。。。。。3分
平面EDB。 。。。。。。。。。。。。。。3分
(II)证明:![]() 底在ABCD且
底在ABCD且![]() 底面ABCD,
底面ABCD,![]()
![]() ①
①
同样由![]() 底面ABCD,得
底面ABCD,得![]()
![]() 底面ABCD是正方形,有
底面ABCD是正方形,有![]() 平面PDC
平面PDC
而![]() 平面PDC,
平面PDC,![]() ② 。。。。。。。。。。。。。。6分
② 。。。。。。。。。。。。。。6分
由①和②推得![]() 平面PBC
平面PBC
而![]() 平面PBC,
平面PBC,![]()
又![]() 且
且![]() ,所以
,所以![]() 平面EFD 。。。。。。。。。。。。。。。。8分
平面EFD 。。。。。。。。。。。。。。。。8分
(III)解:由(II)知,![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角
的平面角
由(II)知,![]()
设正方形ABCD的边长为![]() ,则
,则![]()
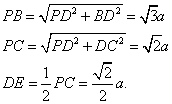
在![]() 中,
中,
![]() 。。。。。。。。。。。。10分
。。。。。。。。。。。。10分
在![]() 中,
中,
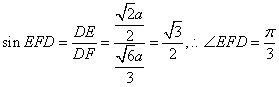
所以,二面角![]() 的大小为
的大小为![]()
方法二:如图所示建立空间直角坐标系,D为坐标原点。设![]()
|
(I)证明:连结AC,AC交BD于G。连结EG。
依题意得![]()
![]() 底面ABCD是正方形,
底面ABCD是正方形,
![]()
![]() 是此正方形的中心,
是此正方形的中心,
![]() 故点G的坐标为
故点G的坐标为![]() 且
且
![]()
![]() 。这表明
。这表明![]() 。
。
而![]() 平面EDB且
平面EDB且![]() 平面EDB,
平面EDB,![]() 平面EDB。
平面EDB。
(II)证明:依题意得![]() 。又
。又![]() 故
故
![]()
![]()
由已知![]() ,且
,且![]() 所以
所以![]() 平面EFD。
平面EFD。
(III)解:设点F的坐标为![]() 则
则
![]()
从而 ![]() 所以
所以
![]()
由条件![]() 知,
知,![]() 即
即
![]() 解得
解得 ![]() 。
。
![]() 点F的坐标为
点F的坐标为![]() 且
且
![]()
![]()
即![]() ,故
,故![]() 是二面角
是二面角![]() 的平面角。
的平面角。
![]() 且
且

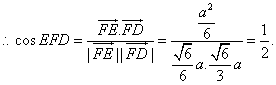
![]()
所以,二面角![]() 的大小为
的大小为![]()


科目:高中数学 来源: 题型:
(04年天津卷理)(12分)
从4名男生和2名女生中任选3人参加演讲比赛。设随机变量![]() 表示所选3人中女生的人数。
表示所选3人中女生的人数。
(I) 求![]() 的分布列;
的分布列;
(II) 求![]() 的数学期望;
的数学期望;
(III) 求“所选3人中女生人数![]() ”的概率。
”的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年天津卷理)(12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]()
其中![]() 为常数,
为常数,![]() 为非零常数。
为非零常数。
(I)令![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)当![]() 时,求
时,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年天津卷理)(14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]() 的准线
的准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(I) 求椭圆的方程及离心率;
(II)若![]() 求直线PQ的方程;
求直线PQ的方程;
(III)设![]() ,过点P且平行于准线
,过点P且平行于准线![]() 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明
![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com