
°æƒø°ø»ÁÕºÀ˘ 棨 ![]() «ƒ≥∫£Õ¬√”Œ«¯µƒ“ªΩ«£¨∆‰÷–
«ƒ≥∫£Õ¬√”Œ«¯µƒ“ªΩ«£¨∆‰÷–![]() £¨Œ™¡À”™‘Ï∏¸º””≈√¿µƒ¬√”Œª∑æ≥£¨¬√”Œ«¯πЌت·æˆ∂®‘⁄÷±œþ∫£∞∂
£¨Œ™¡À”™‘Ï∏¸º””≈√¿µƒ¬√”Œª∑æ≥£¨¬√”Œ«¯πЌت·æˆ∂®‘⁄÷±œþ∫£∞∂![]() ∫Õ
∫Õ![]() …œ∑÷±–ÞΩ®π€π‚≥§¿»
…œ∑÷±–ÞΩ®π€π‚≥§¿»![]() ∫ÕAC£¨∆‰÷–
∫ÕAC£¨∆‰÷–![]() «øÌ≥§¿»£¨‘Ϻ€ «
«øÌ≥§¿»£¨‘Ϻ€ «![]() ‘™/√◊£¨
‘™/√◊£¨ ![]() «’≠≥§¿»£¨‘Ϻ€ «
«’≠≥§¿»£¨‘Ϻ€ «![]() ‘™/√◊£¨¡Ω∂Œ≥§¿»µƒ◊БϺ€Œ™120ÕÚ‘™£¨Õ¨ ±‘⁄œþ∂Œ
‘™/√◊£¨¡Ω∂Œ≥§¿»µƒ◊БϺ€Œ™120ÕÚ‘™£¨Õ¨ ±‘⁄œþ∂Œ![]() …œøøΩ¸µ„
…œøøΩ¸µ„![]() µƒ»˝µ»∑÷µ„
µƒ»˝µ»∑÷µ„![]() ¥¶Ω®“ª∏ˆπ€π‚∆Ω≤¢Ω®ÀÆ…œ÷±œþÕ®µ¿
¥¶Ω®“ª∏ˆπ€π‚∆Ω≤¢Ω®ÀÆ…œ÷±œþÕ®µ¿![]() £®∆Ωî¥Û–°∫ˆ¬‘≤ªº∆£©£¨ÀÆ…œÕ®µ¿µƒ‘Ϻ€ «
£®∆Ωî¥Û–°∫ˆ¬‘≤ªº∆£©£¨ÀÆ…œÕ®µ¿µƒ‘Ϻ€ «![]() ‘™/√◊£Æ
‘™/√◊£Æ
(1) »ÙπʪƑ⁄»˝Ω«–Œ![]() «¯”Úƒ⁄ø™∑¢ÀÆ…œ”Œ¿÷œÓƒø£¨“™«Û
«¯”Úƒ⁄ø™∑¢ÀÆ…œ”Œ¿÷œÓƒø£¨“™«Û![]() µƒ√ʪ˝◊Ó¥Û£¨ƒ«√¥
µƒ√ʪ˝◊Ó¥Û£¨ƒ«√¥![]() ∫Õ
∫Õ![]() µƒ≥§∂»∑÷±Œ™∂ý…Ÿ√◊£ø
µƒ≥§∂»∑÷±Œ™∂ý…Ÿ√◊£ø
(2) ‘⁄(1)µƒÃıº˛œ¬£¨Ω®÷±œþÕ®µ¿![]() ªπ–Ë“™∂ý…Ÿ«Æ£ø
ªπ–Ë“™∂ý…Ÿ«Æ£ø
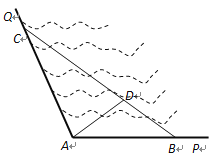
°æ¥∞∏°ø£®1£©![]() ∫ÕACµƒ≥§∂»∑÷±Œ™750√◊∫Õ1500√◊£®2£©
∫ÕACµƒ≥§∂»∑÷±Œ™750√◊∫Õ1500√◊£®2£©![]() ÕÚ‘™
ÕÚ‘™
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©…Ë![]() ≥§Œ™
≥§Œ™![]() √◊£¨
√◊£¨ ![]() ≥§Œ™
≥§Œ™![]() √◊£¨“¿Ã‚“‚µ√
√◊£¨“¿Ã‚“‚µ√![]() £¨º¥
£¨º¥![]() £¨±Ì æ√ʪ˝,¿˚”√ª˘±æ≤ªµ» Ωø…µ√Ω·¬€£ª£®2£©¿˚”√œÚ¡ø∑Ω∑®£¨Ω´
£¨±Ì æ√ʪ˝,¿˚”√ª˘±æ≤ªµ» Ωø…µ√Ω·¬€£ª£®2£©¿˚”√œÚ¡ø∑Ω∑®£¨Ω´![]() ±Ì 挙
±Ì 挙![]() £¨∏˘æðœÚ¡øµƒ ˝¡øª˝”΃£≥§µƒπÿœµø…µ√Ω·π˚.
£¨∏˘æðœÚ¡øµƒ ˝¡øª˝”΃£≥§µƒπÿœµø…µ√Ω·π˚.
‘Ã‚Ω‚Œˆ£∫£®1£©…Ë![]() ≥§Œ™
≥§Œ™![]() √◊£¨
√◊£¨ ![]() ≥§Œ™
≥§Œ™![]() √◊£¨“¿Ã‚“‚µ√
√◊£¨“¿Ã‚“‚µ√![]() £¨
£¨
º¥![]() £¨
£¨
![]()
![]()
![]()
![]() =
=![]()
![]()
µ±«“Ωˆµ±![]() £¨º¥
£¨º¥![]() ±µ»∫≈≥…¡¢£¨
±µ»∫≈≥…¡¢£¨
À˘“‘µ±![]() µƒ√ʪ˝◊Ó¥Û ±£¨
µƒ√ʪ˝◊Ó¥Û ±£¨ ![]() ∫ÕACµƒ≥§∂»∑÷±Œ™750√◊∫Õ1500√◊
∫ÕACµƒ≥§∂»∑÷±Œ™750√◊∫Õ1500√◊
![]() £Æ
£Æ
”…![]()
µ√![]()
![]()
![]()
![]()
![]() £¨
£¨
![]() ‘™
‘™
À˘“‘£¨Ω®ÀÆ…œÕ®µ¿![]() ªπ–Ë“™
ªπ–Ë“™![]() ÕÚ‘™£Æ
ÕÚ‘™£Æ
Ω‚∑®∂˛£∫‘⁄![]() ÷–£¨
÷–£¨ ![]()
![]()
![]()
‘⁄![]() ÷–£¨
÷–£¨ ![]()
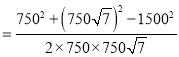
![]()
‘⁄![]() ÷–£¨
÷–£¨ ![]()
![]() =
=![]()
![]() ‘™
‘™
À˘“‘£¨Ω®ÀÆ…œÕ®µ¿![]() ªπ–Ë“™
ªπ–Ë“™![]() ÕÚ‘™£Æ
ÕÚ‘™£Æ
Ω‚∑®»˝£∫“‘AŒ™‘≠µ„£¨“‘ABŒ™![]() ÷·Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨‘Ú
÷·Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨‘Ú![]() £¨
£¨ ![]()
![]() ,º¥
,º¥![]() £¨…Ë
£¨…Ë![]()
”…![]() £¨«Ûµ√
£¨«Ûµ√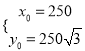 £¨ À˘“‘
£¨ À˘“‘![]()
À˘“‘£¨ ![]()
![]()
![]() ‘™
‘™
À˘“‘£¨Ω®ÀÆ…œÕ®µ¿![]() ªπ–Ë“™
ªπ–Ë“™![]() ÕÚ‘™£Æ
ÕÚ‘™£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC÷–£¨a°¢b°¢c∑÷± «°œA°¢°œB°¢°œCµƒ∂‘±þ≥§£¨“—÷™a°¢b°¢c≥…µ»±» ˝¡–£¨«“a2©Åc2=ac©Åbc£¨
£®1£©«Û°œAµƒ¥Û–°£ª
£®2£©«Û ![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë÷±œþ![]() ”Î≈◊ŒÔœþ
”Î≈◊ŒÔœþ![]() œýΩª”⁄≤ªÕ¨¡Ωµ„
œýΩª”⁄≤ªÕ¨¡Ωµ„![]() °¢
°¢![]() £¨”Α≤
£¨”Α≤![]() œý«–”⁄µ„
œý«–”⁄µ„![]() £¨«“
£¨«“![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() ÷–µ„£Æ
÷–µ„£Æ
(1) »Ù![]() «’˝»˝Ω«–Œ£®
«’˝»˝Ω«–Œ£®![]() «◊¯±Í‘≠µ„£©£¨«Û¥À»˝Ω«–Œµƒ±þ≥§£ª
«◊¯±Í‘≠µ„£©£¨«Û¥À»˝Ω«–Œµƒ±þ≥§£ª
(2) »Ù![]() £¨«Û÷±œþ
£¨«Û÷±œþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
(3) ‘∂‘![]() Ω¯––Ã÷¬€£¨«Îƒ„–¥≥ˆ∑˚∫œÃıº˛µƒ÷±œþ
Ω¯––Ã÷¬€£¨«Îƒ„–¥≥ˆ∑˚∫œÃıº˛µƒ÷±œþ![]() µƒÃı ˝£®÷±Ω”–¥≥ˆΩ·¬€£©£Æ
µƒÃı ˝£®÷±Ω”–¥≥ˆΩ·¬€£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂®“‘⁄R…œµƒ∫Ø ˝f£®x£©¬˙◊„£∫f£®x£©= ![]() £¨«“f£®x+2£©=f£®x£©£¨g£®x£©=
£¨«“f£®x+2£©=f£®x£©£¨g£®x£©= ![]() £¨‘Ú∑Ω≥Ãf£®x£©=g£®x£©‘⁄«¯º‰[©Å5£¨1]…œµƒÀ˘”– µ∏˘÷Æ∫ÕŒ™£® £©
£¨‘Ú∑Ω≥Ãf£®x£©=g£®x£©‘⁄«¯º‰[©Å5£¨1]…œµƒÀ˘”– µ∏˘÷Æ∫ÕŒ™£® £©
A.©Å5
B.©Å6
C.©Å7
D.©Å8
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=Asin£®¶ÿx+¶’£©£¨x° R£®∆‰÷–A£æ0£¨¶ÿ£æ0£¨0£º¶’£º ![]() £©µƒÕºœÛ”Îx÷·µƒΩªµ„÷–£¨œý¡⁄¡Ω∏ˆΩªµ„÷ƺ‰µƒæý¿ÎŒ™
£©µƒÕºœÛ”Îx÷·µƒΩªµ„÷–£¨œý¡⁄¡Ω∏ˆΩªµ„÷ƺ‰µƒæý¿ÎŒ™ ![]() £¨«“ÕºœÛ…œ“ª∏ˆ◊Ó∏þµ„Œ™M£®
£¨«“ÕºœÛ…œ“ª∏ˆ◊Ó∏þµ„Œ™M£® ![]() £¨3£©£Æ
£¨3£©£Æ
£®1£©«Ûf£®x£©µƒΩ‚Œˆ Ω£ª
£®2£©œ»∞—∫Ø ˝y=f£®x£©µƒÕºœÛœÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª≥§∂»£¨»ª∫Û‘Ÿ∞—À˘µ√ÕºœÛ…œ∏˜µ„µƒ∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©£¨µ√µΩ∫Ø ˝y=g£®x£©µƒÕºœÛ£¨ ‘–¥≥ˆ∫Ø ˝y=g£®x£©µƒΩ‚Œˆ Ω£Æ
∏ˆµ•Œª≥§∂»£¨»ª∫Û‘Ÿ∞—À˘µ√ÕºœÛ…œ∏˜µ„µƒ∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£®◊ð◊¯±Í≤ª±‰£©£¨µ√µΩ∫Ø ˝y=g£®x£©µƒÕºœÛ£¨ ‘–¥≥ˆ∫Ø ˝y=g£®x£©µƒΩ‚Œˆ Ω£Æ
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ù◊Хʑ⁄x0° [©Å ![]() £¨
£¨ ![]() ]£¨ πµ√≤ªµ» Ωg£®x0£©+2°Ðlog3m≥…¡¢£¨«Û µ ˝mµƒ◊Ó–°÷µ£Æ
]£¨ πµ√≤ªµ» Ωg£®x0£©+2°Ðlog3m≥…¡¢£¨«Û µ ˝mµƒ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™‘⁄![]() ÷–£¨Ω«
÷–£¨Ω«![]() µƒ∂‘±þ∑÷±Œ™
µƒ∂‘±þ∑÷±Œ™![]() ,«“
,«“![]() .
.
£®1£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»Ù![]() ,«Û
,«Û![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∫Ø ˝f£®x£©=4cos2x©Å4 ![]() sinxcosxµƒ◊Ó–°’˝÷Ð∆⁄Œ™¶–£®£æ0£©£Æ
sinxcosxµƒ◊Ó–°’˝÷Ð∆⁄Œ™¶–£®£æ0£©£Æ
£®1£©«Ûµƒ÷µ£ª
£®2£©»Ùf£®x£©µƒ∂®“”ڌ™[©Å ![]() £¨
£¨ ![]() ]£¨«Ûf£®x£©µƒ◊Ó¥Û÷µ”Î◊Ó–°÷µº∞œý”¶µƒxµƒ÷µ£Æ
]£¨«Ûf£®x£©µƒ◊Ó¥Û÷µ”Î◊Ó–°÷µº∞œý”¶µƒxµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∫Ø ˝![]() £Æ
£Æ
£®¢Ò£©»Ù![]() £¨«Û
£¨«Û![]() ‘⁄«¯º‰[-1,2]…œµƒ»°÷µ∑∂Œß£ª
‘⁄«¯º‰[-1,2]…œµƒ»°÷µ∑∂Œß£ª
£®¢Ú£©»Ù∂‘»Œ“‚![]() £¨
£¨ ![]() ∫„≥…¡¢£¨º«
∫„≥…¡¢£¨º«![]() £¨«Û
£¨«Û![]() µƒ◊Ó¥Û÷µ£Æ
µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ª∏ˆæ˘‘»µƒ’˝∑ΩÃÂÕÊæþ£¨∏˜∏ˆ√Ê…œ∑÷±–¥”–1£¨2£¨3£¨4£¨5£¨6£¨Ω´’‚∏ˆÕÊæþœ»∫Û≈◊÷¿2¥Œ£¨«Û£∫
£®1£©≥Ø…œµƒ“ª√Ê ˝œýµ»µƒ∏≈¬ £ª
£®2£©≥Ø…œµƒ“ª√Ê ˝÷Æ∫Õ–°”⁄5µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com