
��22��
������������ͬ����������ֽƬ����ͼ1��ͼ2����Ҫ��������һ���ƴ��һ��������ģ�ͣ���һ���ƴ��һ����������ģ�ͣ�ʹ���ǵ�ȫ�������ԭ�����ε������ȣ������һ�ּ�ƴ�������ֱ������߱�ʾ��ͼ1��ͼ2�У�������Ҫ˵����
�����ԱȽ����ƴ������������������������Ĵ�С��
���������������һ�����������ε�ֽƬ����ͼ3����Ҫ���ƴ��һ��ֱ������ģ�ͣ�ʹ����ȫ���������������ε������ȣ������һ�ּ�ƴ�����������߱�ʾ��ͼ3�У�������Ҫ˵��.
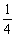
��22����С����Ҫ����ռ��������������ֲ���������̽�����������������ѧ֪ʶ�����ʵ���������.
�⣺
������ͼ1�����������������е��������𣬿�ƴ��һ��������.������������������������������������������������
��ͼ2�����������������ϼ���������ͬ���ı��Σ���ϳ���һ���ڱ߱߳�Ϊ�����α߳���![]() ����һ��Խ�Ϊֱ��.���²��ְ��������𣬿ɳ�Ϊһ��ȱ�ϵ�������������������������ͬ���ı���ǡ��ƴ����������������ϵ�.������������������������
����һ��Խ�Ϊֱ��.���²��ְ��������𣬿ɳ�Ϊһ��ȱ�ϵ�������������������������ͬ���ı���ǡ��ƴ����������������ϵ�.������������������������
�����������ƴ�ķ�������V����V.
�������£�
�������������ֽƬ�ı߳�Ϊ2����ô�������������������ĵ��涼�DZ߳�Ϊ1���������Σ������Ϊ![]() .���ڼ������ǵĸߣ�
.���ڼ������ǵĸߣ�
h=![]() =
=![]() ��
��
h��=![]() tan30��=
tan30��=![]() .
.
��V��V��=��![]() h��h������
h��h������![]()
=��![]() ��
��![]() ����
����![]() =
=![]() ��0��
��0��
��V����V. ������������������������������������������
������ͼ3���ֱ����������ε�����������㣬�õ������߶Σ������������߶ε��е�Ϊ������������.��������������Ϊֱ�������ĵ��棬���������ε�����������ԭ���������������ߣ������������������ı��Σ�����ƴ�ӳ�ֱ���������ϵף����²��ְ��������𣬳�Ϊһ��ȱ�ϵ�ֱ�����������ɵõ�ֱ������ģ��.
ע���������������ļ�ƴ�������ɱ��ձ�������.


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an+an+2 |
| 2 |
| 1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 6 |
| 2 |
| sin2x |
| 2 |
| 1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
|
log
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com