
【题目】给出以下四个命题:
①已知命题p:x∈R,tanx=2;命题q:x∈R,x2﹣x+1≥0,则命题p∧q是真命题;
②过点(﹣1,2)且在x轴和y轴上的截距相等的直线方程是x+y﹣1=0;
③函数f(x)=2x+2x﹣3在定义域内有且只有一个零点;
④若直线xsin α+ycos α+l=0和直线 ![]() 垂直,则角
垂直,则角 ![]() .
.
其中正确命题的序号为 . (把你认为正确的命题序号都填上)
【答案】①③
【解析】解:对于①,根据正切的定义知命题p是真命题,
而命题q:x∈R,x2﹣x+1≥0,因为△=(﹣1)2﹣4×1×1=﹣3<0,
所以抛物线y=x2﹣x+1开口向上并且与x轴无公共点,故p也是真命题.
因此命题p∧q是真命题,①正确;
对于②,过点(﹣1,2)且在x轴和y轴上的截距相等的直线方程除了x+y﹣1=0还有y=﹣2x,故②不正确;
对于③,f(x)=2x+2x﹣3在R上是增函数,而且f(0)=﹣2<0,f(1)=1>0
所以函数f(x)=2x+2x﹣3在定义域内有且只有一个零点,故③是真命题;
对于④,直线xsin α+ycos α+l=0和直线 ![]() 垂直,则sinαcosα﹣
垂直,则sinαcosα﹣ ![]() cosα=0,
cosα=0,
可得sinα= ![]() 或cosα=0,所以α=2kπ+
或cosα=0,所以α=2kπ+ ![]() 或α=2kπ+
或α=2kπ+ ![]() 或α=kπ+
或α=kπ+ ![]()
由此可得④不正确.
所以答案是:①③
【考点精析】利用复合命题的真假和特称命题对题目进行判断即可得到答案,需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真;特称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;特称命题的否定是全称命题.
;特称命题的否定是全称命题.


科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为 ![]() .
. 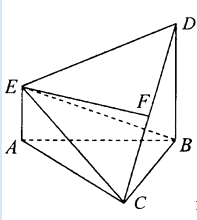
(1)若F是线段CD的中点,证明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 为平面上动点,过点
为平面上动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,在
两点,在![]() 处分别作轨迹
处分别作轨迹![]() 的切线交于点
的切线交于点![]() ,设直线
,设直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)为二次函数,若y=f(x)在x=2处取得最小值﹣4,且y=f(x)的图象经过原点,
(1)求f(x)的表达式;
(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,且AC=BD,平面PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)在△PAD中,AP=2,AD=2 ![]() ,PD=4,三棱锥E﹣ACD的体积是
,PD=4,三棱锥E﹣ACD的体积是 ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com