
思路:只要在已知中给出了直径这一条件,不仅要想到它和半径的关系,还要想到封闭了它所对的圆周角,便得到了直角三角形,这样有关直角三角形的性质便可应用了.
探究:如图2-1-7,以CD为直径的⊙O交△ACD的两边于B、E,连结BE.求证:ADcosA=AB.此题必须先证AD、AB所在的△ABD为直角三角形,此时连结BD,可由直径所对的圆周角为90°,创造所需的条件.又如图2-1-8,在⊙O中,直径AB⊥CD,弦AE⊥CF.要证△ABE≌△CDF,在已知∠A=∠C,AB=CD以后,还缺少一个条件,由AB、CD为直径,想到连结BE、CF,便可知∠E=∠F=90°,这就为证三角形全等提供了条件.
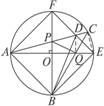
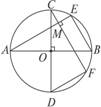
图2-1-7 图2-1-8


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:填空题
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)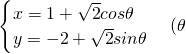 是参数)相切,则b=________.
是参数)相切,则b=________.查看答案和解析>>
科目:高中数学 来源:2012年陕西省宝鸡市高三教学质量检测数学试卷3(文科)(解析版) 题型:解答题
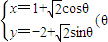 是参数)相切,则b= .
是参数)相切,则b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com