【题目】在平面直角坐标系xOy中，已知椭圆
1（a＞b＞0）的焦距F1F2的长为2，经过第二象限内一点P（m，n）的直线
1与圆x2+y2＝a2交于A，B两点，且OA
．
（1）求PF1+PF2的值；
（2）若
，求m，n的值．
【答案】（1）2
．（2）m＝﹣1，n
．
【解析】
（1）先说明点P在椭圆上，根据椭圆性质即可得解；
（2）设A（x1，y1），B（x2，y2），联立方程组得x1+x2
，x1x2
，转化条件得x2﹣x1
，代入解方程即可得解.
（1）∵OA
，∴a．
∵把点P（m，n）代入直线方程
1，可得：
1，
∴点P在椭圆上，
∴PF1+PF2＝2a＝2
．
（2）由a，c＝1，∴b2＝a2﹣c2＝1．
设A（x1，y1），B（x2，y2）．
联立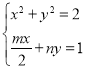
，化为：（4n2+m2）x2﹣4mx+4﹣8n2＝0，
∴x1+x2，x1x2．
∵
，∴（x2﹣x1，y2﹣y1）（2，0）
，
化为2（x2﹣x1），即x2﹣x1
，
∴
4x1x2
，
代入可得：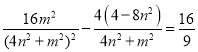
，
化为：56n4+10n2m2﹣36n2﹣m4＝0，
又
1，
把m2＝2﹣2n2代入化为8n4﹣2n2﹣1＝0，
解得m2＝1，n2
．
∵点P在第二象限，
∴取m＝﹣1，n．
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案科目：高中数学 来源： 题型：
【题目】已知函数
， 
.
（Ⅰ）若
，求函数
在
的单调区间；
（Ⅱ）方程
有3个不同的实根，求实数
的取值范围；
（Ⅲ）当
时，若对于任意的
，都存在
，使得
，求满足条件的正整数
的取值的集合.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示的多面体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，CM⊥AB，垂足为M，且AE＝AC＝2
，BD＝2BC＝4，
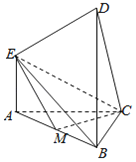
（1）求证：CM⊥ME；
（2）求二面角A﹣MC﹣E的余弦值．
（3）在线段DC上是否存在一点N，使得直线BN∥平面EMC，若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在棱长为
的正方体
中，O是AC的中点，E是线段D1O上一点，且D1E＝λEO.
（1）若λ=1，求异面直线DE与CD1所成角的余弦值;
（2）若平面CDE⊥平面CD1O，求λ的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：x∈[1，2]，log2（x+2）＜2m；命题q：关于x的方程x2﹣x+m2＝0有两个不同的实数根.
（1）若（￢p）∧q为真命题，求实数m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程：在平面直角坐标系
中，曲线
：
（
为参数），在以平面直角坐标系的原点为极点、
轴的正半轴为极轴，且与平面直角坐标系取相同单位长度的极坐标系中，曲线
：
.
（1）求曲线的普通方程以及曲线的平面直角坐标方程；
（2）若曲线上恰好存在三个不同的点到曲线的距离相等，求这三个点的极坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的奇数项是首项为
的等差数列，偶数项是首项为
的等比数列．数列前
项和为
，且满足
，
．
（1）求数列的通项公式；
（2）若
，求正整数
的值；
（3）是否存在正整数，使得
恰好为数列中的一项？若存在，求出所有满足条件的值，若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
