解:(1)对于函数f
1(x)=|x-1|+|x-2|,当x∈[1,2]时,f
1(x)=1.
当x<1或x>2时,f
1(x)>|(x-1)-(x-2)|=1恒成立,
故f
1(x)是“平底型”函数. (2分)
对于函数f
2(x)=x+|x-2|,
当x∈(-∞,2]时,f
2(x)=2;
当x∈(2,+∞)时,f
2(x)=2x-2>2.
所以不存在闭区间[a,b],使当x∉[a,b]时,f(x)>2恒成立.
故f
2(x)不是“平底型”函数. (4分)
(2)因为函数
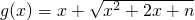
是区间[-2,+∞)上的“平底型”函数,
则存在区间[a,b]⊆[-2,+∞)和常数c,
使得
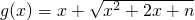
=c恒成立.
所以x
2+2x+n=(x-c)
2恒成立,
∴c=-1,n=1,g(x)=x+|x+1|.
当x∈[-2,-1]时,g(x)=-1,当x∈(-1,+∞)时,g(x)=2x+1>-1恒成立.
此时,g(x)是区间[-2,+∞)上的“平底型”函数,n=1为所求.
(3)若|t-k|+|t+k|≥|k|•f(x)对一切t∈R恒成立,
则(|t-k|+|t+k|)
min≥|k|•f(x).
因为(|t-k|+|t+k|)
min=2|k|,
所以2|k|≥|k|•f(x).又k≠0,则f(x)≤2.
则|x-1|+|x-2|≤2,解得

.
故实数x的范围是
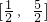
.
分析:(1)对于函数f
1(x)=|x-1|+|x-2|,当x∈[1,2]时,f
1(x)=1,当x∉[1,2]时,f
1(x)>|(x-1)-(x-2)|=1恒成立,f
1(x)可以判断了;同理可判断f
2(x)不是“平底型”函数;
(2)首先由于恒有g(x)=c,所以根号里的式子必须要能开方开出来,即为完全平方,可求得n=1;
(3)由于f(x)是“平底型”函数,不等式|t-k|+|t+k|≥|k|•f(x)对一切t∈R恒成立,只需(|t-k|+|t+k|)
min≥|k|•f(x)即可,而(|t-k|+|t+k|)
min=2|k|,问题解决.
点评:本题考查函数恒成立的问题,解决本题的灵魂在于“转化”,将含有绝对值的问题转化为不含绝对值的问题,使问题在实施“化难为易”、“化生为熟”中得以解决.

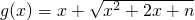 是区间[-2,+∞)上的“平底型”函数,求n的值.
是区间[-2,+∞)上的“平底型”函数,求n的值.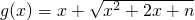 是区间[-2,+∞)上的“平底型”函数,
是区间[-2,+∞)上的“平底型”函数,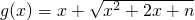 =c恒成立.
=c恒成立. .
.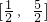 .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案