
已知![]() ,点B是
,点B是![]() 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线![]() 交
交![]()
![]() 轴于点Q,若
轴于点Q,若
![]() ,
,![]() .
.
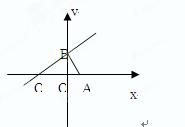
(1)求点P的轨迹方程;
(2)是否存在定直线![]() ,以PM为直径的圆与直线
,以PM为直径的圆与直线![]() 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
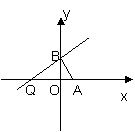 解: (1)设B(0,t),设Q(m,0),t2=
解: (1)设B(0,t),设Q(m,0),t2=![]() |m|,
|m|,![]() m
m![]() 0, m=-4t2,
0, m=-4t2,
![]() Q(-4t2,0),设P(x,y),则
Q(-4t2,0),设P(x,y),则![]() =(x-
=(x-![]() ,y),
,y),![]() =(-4t2-
=(-4t2-![]() ,0),
,0),
2![]() =(-
=(-![]() ,2 t),
,2 t), ![]()
![]() +
+![]() =2
=2![]() 。
。
![]() (x-
(x-![]() ,y)+ (-4t2-
,y)+ (-4t2-![]() ,0)= (-
,0)= (-![]() ,2 t),
,2 t),
![]() x=4t2,y=2 t,
x=4t2,y=2 t,![]() y2=x,此即点P的轨迹方程;…………………6分。
y2=x,此即点P的轨迹方程;…………………6分。
(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),![]() M (4,0) ,则以PM为直径的圆的圆心即PM的中点T(
M (4,0) ,则以PM为直径的圆的圆心即PM的中点T(![]() ,
,![]() ), 以PM为直径的圆与直线x=a的相交弦长:
), 以PM为直径的圆与直线x=a的相交弦长:
L=2![]()
=2![]() =2
=2![]() ……………10分
……………10分
若a为常数,则对于任意实数y,L为定值的条件是a-![]() =0, 即a=
=0, 即a=![]() 时,L=
时,L=![]()
![]() 存在定直线x=
存在定直线x=![]() ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x=![]() 的相交弦长为定值
的相交弦长为定值![]() 。
。
(2)存在定直线x=![]() ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x=![]() 的相交弦长为定值
的相交弦长为定值![]() 。
。


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:2014届吉林省白山市高三摸底考试理科数学试卷(解析版) 题型:解答题
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.

(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届吉林省白山市高三摸底考试文科数学试卷(解析版) 题型:解答题
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.

(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2013年湖南省长沙市高考模拟文科数学试卷(解析版) 题型:解答题
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若
 ,
, .
.

(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省长沙市高三高考模拟理科数学试卷(解析版) 题型:解答题
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交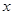 轴于点Q,若
轴于点Q,若
 ,
, .
.

(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com