【题目】判断下列命题是否正确（正确的在括号内打“√”，错误的打“×”）.
（1）
.（________）
（2）
.（________）
（3）
.（________）
（4）
.（________）
科目：高中数学 来源： 题型：
【题目】已知椭圆
经过点
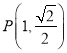，且离心率为
.
（1）求椭圆
的方程；
（2）设
分别为椭圆
的左、右焦点，不经过
的直线
与椭圆
交于两个不同的点
，如果直线
、
、
的斜率依次成等差数列，求焦点
到直线
的距离
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
，
，
是
的动点，过点作的垂线，线段
的中垂线交
于点
，的轨迹为
.
(1)求轨迹的方程；
(2)过
且与坐标轴不垂直的直线交曲线于
两点，若以线段
为直径的圆与直线
相切，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关，在某医院随机对心肺疾病入院的
人进行问卷调查，得到了如下的列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
（1）用分层抽样的方法在患心肺疾病的人群中抽
人，其中男性抽多少人？
（2）在上述抽取的
人中选
人，求恰好有
名女性的概率；
（3）为了研究心肺疾病是否与性别有关，请计算出统计量
，你有多大把握认为心肺疾病与性别有关？
下面的临界值表供参考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式： 
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（12分）
如图，四边形ABCD为梯形，AB//CD，
平面ABCD，
为BC的中点.
（1）求证：平面
平面PDE.
（2）在线段PC上是否存在一点F，使得PA//平面BDF？若存在，指出点F的位置，并证明；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产甲，乙两种图画纸，计划每种图画纸的生产量不少于8t，已知生产甲种图画纸1t要用芦苇7t、黄麻3t、枫树5t；生产乙种图画纸1t要用芦苇3t、黄麻4t、枫树8 t.现在仓库内有芦苇300t、黄麻150t.枫树200t，试列出满足题意的不等式组.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=
sinxcosx+cos2x-
．
（Ⅰ）求函数f（x）的最小正周期及单调递增区间；
（Ⅱ）将函数f（x）图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数g（x）的图象．若关于x的方程g（x）-k=0，在区间[0，
]上有实数解，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】校园准备绿化一块直径为
的半圆形空地，点
在半圆圆弧上，△
外的地方种草，△的内接正方形
为一水池（
，
在边上），其余地方种花，若
， 
，设△的面积为
，正方形面积为
；
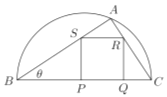
（1）用
和
表示和；
（2）当固定，变化时，求
最小值及此时的角；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某旅游风景区发行的纪念章即将投放市场，根据市场调研情况，预计每枚该纪念章的市场价y（单位：元）与上市时间x（单位：天）的数据如下：
上市时间x天 | 2 | 6 | 20 |
市场价y元 | 102 | 78 | 120 |
（1）根据上表数据，从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由：①
；②
；③
；
（2）利用你选取的函数，求该纪念章市场价最低时的上市天数及最低的价格；
（3）利用你选取的函数，若存在
，使得不等式
成立，求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
