已知数列{an}满足an=2an-1-2n+5(n∈N+且n≥2),a1=1.
(1)若bn=an-2n+1,求证:数列{bn}(n∈N+)是常数列,并求{an}的通项;
(2)若Sn是数列{an}的前n项和,又cn=(-1)nSn,且{cn}的前n项和Tn>tn2在n∈N+时恒成立,求实数t的取值范围.
【答案】
分析:(1)由已知中数列{a
n}满足a
n=2a
n-1-2n+5(n∈N
+且n≥2),a
1=1.我们易得到a
n-2n+1=2[a
n-1-2(n-1)+1],又由b
n=a
n-2n+1,可得b
n=2b
n-1,且b
1=0,进而易判断出数列{b
n}(n∈N
+)是常数列,即b
n=0,再由b
n=a
n-2n+1,即可给出数列{a
n}的通项公式;
(2)由(1)中结论,我们易得数列{a
n}为等差数列,进而易得到S
n的表达式,根据c
n=(-1)
nS
n,求出对应的{c
n}后,分n为奇数和偶数两种情况分别求出T
n解对应的不等式式,即可求出实数t的取值范围.
解答:解:(1)由a
n=2a
n-1-2n+5知:a
n-2n+1=2[a
n-1-2(n-1)+1],而a
1=1
于是由b
n=a
n-2n+1,可知:b
n=2b
n-1,且b
1=0
从而b
n=0,故数列{b
n}是常数列.
于是a
n=2n-1.(5分)
(2)S
n是{a
n}前n项和,则S
n=1+3+5+…+(2n-1)=n
2,c
n=(-1)
nn
2当n为奇数时,即n=2k-1,T
n=T
2k-1=-1
2+2
2-3
2+4
2+…+(2k-2)
2-(2k-1)
2=-k(2k-1)=-
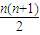
当n为偶数时,T
n=T
2k=T
2k-1+(2k)
2=
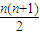
.
∴T
n=
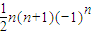
.
由T
n>tn
2恒成立,则需
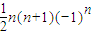
>tn
2恒成立.只需n为奇数时恒成立.
∴
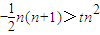
(n=1,3,5,7,),
∴
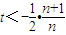
(n=1,3,5,7,)恒成立.
而
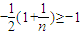
,
∴t<-1,故所需t的范围为(-∞,-1).(13分)
点评:本题考查的知识点是数列递推公式及数列与不等式的综合应用,其中根据已知中数列的递推公式a
n=2a
n-1-2n+5求出数列{a
n}的通项公式是解答本题的关键.

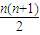
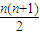 .
.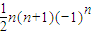 .
.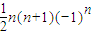 >tn2恒成立.只需n为奇数时恒成立.
>tn2恒成立.只需n为奇数时恒成立.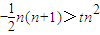 (n=1,3,5,7,),
(n=1,3,5,7,),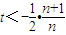 (n=1,3,5,7,)恒成立.
(n=1,3,5,7,)恒成立.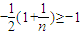 ,
,

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案