
【题目】已知![]() .
.
(1)证明![]() 在
在![]() 处的切线恒过定点;
处的切线恒过定点;
(2)若![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先对函数求导,将![]() 代入导函数中可得切线的斜率,利用点斜式写出切线方程化简得
代入导函数中可得切线的斜率,利用点斜式写出切线方程化简得![]() ,从而可知切线恒过点
,从而可知切线恒过点![]() ;
;
(2)若![]() 有两个极值点,则
有两个极值点,则![]() 有两个不同的正根,即
有两个不同的正根,即![]() 有两个零点,也就是
有两个零点,也就是![]() 的图像与
的图像与![]() 轴有两个交点,然后对
轴有两个交点,然后对![]() 求导,讨论导函数的正负,从而可求出
求导,讨论导函数的正负,从而可求出![]() 单调区间,进而可得到
单调区间,进而可得到![]() 的取值范围
的取值范围
(1)∵![]() ,所以
,所以![]()
又因为![]() ,
,
所以![]() 在
在![]() 处的切线方程
处的切线方程![]()
即![]()
所以![]() 在
在![]() 处的切线恒过定点
处的切线恒过定点![]() .
.
(2)∵![]() ,其中
,其中![]() ,
,
设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
则![]() 在
在![]() 单调递增,
单调递增,
![]() 在
在![]() 上至多有一个零点,
上至多有一个零点,
即![]() 在
在![]() 上至多有一个零点,
上至多有一个零点,
∴![]() 至多只有一个极值点,不合题意,舍去.
至多只有一个极值点,不合题意,舍去.
当![]() 时,设
时,设![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,
,![]() ,
,
∴![]() ,使得
,使得![]() ,即
,即![]() 2,
2,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
∴![]() 在
在![]() 单调递减,
单调递减,
∴![]() 在
在![]() 有极大值
有极大值![]() ,
,
即![]()
![]()
若![]() ,则
,则![]() ,
,
∴![]() ,
,![]() 在
在![]() 单调递减,不合题意,
单调递减,不合题意,
若![]() ,
,
设![]() ,
,![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
又![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,即
,即![]() ,
,
此时![]() ,
,![]()
∵![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,![]()
![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 处取得极小值.
处取得极小值.
又∵![]() ,
,![]()
∴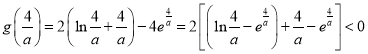
∵![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 处取得极大值.
处取得极大值.
综上所述,若![]() 有两个极值点,则实数
有两个极值点,则实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的极值.
的极值.
(2)![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大值.
的最大值.
(3)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() ?如果存在,请给出证明;如果不存在,请说明理由.
?如果存在,请给出证明;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒蔓延以来,世界各国都在研制疫苗,某专家认为,某种抗病毒药品对新型冠状病毒具有抗病毒、抗炎作用,假如规定每天早上7:00和晚上7:00各服药一次,每次服用该药药量700毫克具有抗病毒功效,若人的肾脏每12小时从体内滤出这种药的70%,该药在人体内含量超过1000毫克,就将产生副作用,若人长期服用这种药,则这种药__________(填“会”或者“不会”)对人体产生副作用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何是一门以不规则几何形态为研究对象的几何学,科赫曲线是比较典型的分形图形,1904年瑞典数学家科赫第一次描述了这种曲线,因此将这种曲线称为科赫曲线.其生成方法是:(I)将正三角形(图(1))的每边三等分,以每边三等分后的中间的那一条线段为一边,向形外作等边三角形,并将这“中间一段”去掉,得到图(2);(II)将图(2)的每边三等分,重复上述的作图方法,得到图(3);(Ⅲ)再按上述方法继续做下去……,设图(1)中的等边三角形的边长为1,并且分别将图(1)、图(2)、图(3)、…、图(n)、…中的图形依次记作![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,设
,…,设![]() 的周长为
的周长为![]() ,则
,则![]() 为( )
为( )
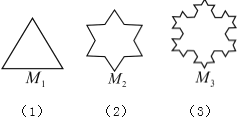
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出以下四个命题:
,给出以下四个命题:
①![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是周期函数;
是周期函数;
④![]() 在
在![]() 上恰有两个零点.
上恰有两个零点.
其中真命题的序号是______.(请写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,直线
轴非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)在(1)中,设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任意一点为
上任意一点为![]() ,当点
,当点![]() 到直线
到直线![]() 的距离取最大值时,求此时点
的距离取最大值时,求此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.
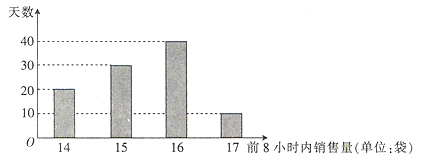
记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com