
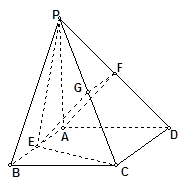
如图,四棱锥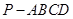 的底面是正方形,
的底面是正方形,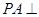 底面
底面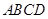 ,
,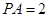 ,
, ,点
,点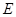 、
、 分别为棱
分别为棱 、
、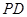 的中点.
的中点.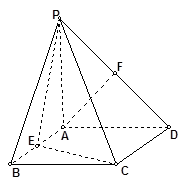
(1)求证: 平面
平面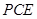 ;
;
(2)求证:平面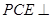 平面
平面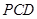 ;
;
(3)求三棱锥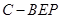 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)三棱锥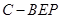 的体积为
的体积为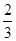 .
.
解析试题分析:(1)取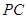 的中点
的中点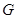 ,连接
,连接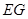 、
、 ,证明四边形
,证明四边形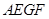 为平行四边形,得到
为平行四边形,得到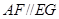 ,再利用直线平面平行的判定定理得到
,再利用直线平面平行的判定定理得到 平面
平面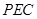 ;(2)先证明
;(2)先证明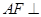 平面
平面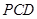 ,利用(1)中的条件
,利用(1)中的条件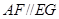 得到
得到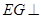 平面
平面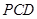 ,再利用平面与平面垂直的判定定理证明平面
,再利用平面与平面垂直的判定定理证明平面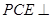 平面
平面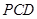 ,在证明
,在证明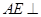 平面
平面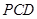 的过程中,在等腰三角形
的过程中,在等腰三角形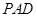 中利用三线合一得到
中利用三线合一得到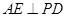 ,通过证明
,通过证明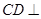 平面
平面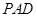 得到
得到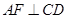 ,然后利用直线与平面垂直的判定定理即可证明
,然后利用直线与平面垂直的判定定理即可证明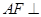 平面
平面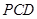 ;(3)利用题中的条件
;(3)利用题中的条件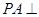 平面
平面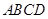 ,在计算三棱锥
,在计算三棱锥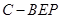 的体积中,选择以点
的体积中,选择以点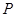 为顶点,
为顶点,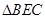 所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为
所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为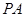 ,最后利用锥体的体积计算公式即可.
,最后利用锥体的体积计算公式即可.
试题解析:(1)取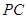 的中点
的中点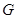 ,连结
,连结 、
、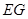 ,
,
∴ 为
为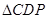 的中位线,
的中位线,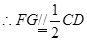 ,
,
∵四边形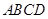 为矩形,
为矩形,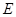 为
为 的中点,
的中点,
∴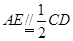 ,
,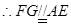 ,
,
∴四边形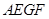 是平行四边形,
是平行四边形,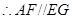 ,
,
又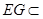 平面
平面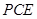 ,
,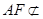 平面
平面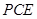 ,
,
∴ 平面
平面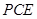 ;
;
(2)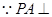 底面
底面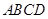 ,
,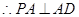 ,
,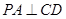 ,又
,又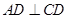 ,
,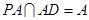 ,
,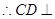 平面
平面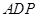 , 又
, 又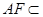 平面
平面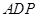 ,
, 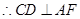 ,
,
直角三角形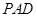 中,
中, ,
,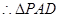 为等腰直角三角形,
为等腰直角三角形,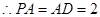 ,
,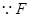 是
是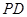 的中点,
的中点,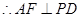 ,又
,又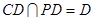 ,
,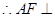 平面
平面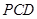 ,
,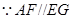 ,
,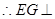 平面
平面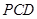 ,
,


科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB. 
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知半径为 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为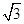 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.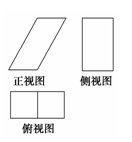
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在直三棱柱 中,
中,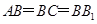 ,
, 为
为 的中点.
的中点.
(Ⅰ) 若AC1⊥平面A1BD,求证:B1C1⊥平面ABB1A1;
(Ⅱ)在(Ⅰ)的条件下,设AB=1,求三棱锥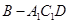 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABC-A1B1C1中,底面为等腰直角三角形,AC⊥BC,点D是AB的中点,侧面BB1C1C是正方形.
(1) 求证AC⊥B1C;(2)求二面角B-CD-B1平面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com