练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年厦门外国语学校模拟）已知方程，则下列结论正确的是                         （     ）

    A．它是奇函数

    B．把它图象的横坐标不变，纵坐标扩大到原来的2倍后的方程是

    C．它的图象是一个封闭图形，且面积小于；

    D．它的图象是一个封闭图形，且面积大于；

    答案：D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    已知数列{an}中，其前n项和为Sn，满足Sn=2an-1，n∈N*，数列{bn}满足bn=1-log
    1
    2
    an，n∈N*
    （1）求数列{an}、{bn}的通项公式；
    （2）设数列{anbn}的n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知{an}是首项为a1=1的等差数列且满足an+1＞an（n∈N*），等比数列{bn}的前三项分别为b1=a1+1，b2=a2+1，b3=a3+3．
    （Ⅰ）求数列{an}和{bn}的通项公式；
    （Ⅱ）若数列{cn}满足（an+3）cnlog2bn=
    1
    2
    ，求数列{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    求和：
    1
    1×4
    +
    1
    4×7
    +…+
    1
    (3n-2)×(3n+1)
    =______．

    查看答案和解析>>

    科目：高中数学 来源：广东省月考题 题型：解答题

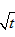    已知数列{an}中，a1=t，a2=t2（t>0且t≠1），若x=是函数f（x）=an-1x3-3[（t+1）an-an+1]x+1（n≥2）的一个极值点。
    （Ⅰ）证明数列{an+1-an}是等比数列，并求数列{an}的通项公式；
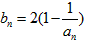    （Ⅱ）记，当t=2时，数列{bn}的前n项和为Sn，求使Sn>2008的n的最小值；
    （Ⅲ）当t=2时，求证：对于任意的正整数n，有。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    练习：求数列
    2
    2
    ，
    4
    22
    ，
    6
    23
    ，…，
    2n
    2n
    …前n项的和．

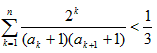    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知数列{an}，{bn}满足a1=2，a2=3，b1=1，且对任意的正整数m，n，p，q，当m+n=p+q时，都有am+bn=ap+bq，设数列{an}前项和为Sn，{bn}前项和为Tn，则
    1
    2011
    (S2011+T2011)    =______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    定义一个“等积数列”：在一个数列中，如果每一项与它后一项的积都是同一常数，那么这个数列叫“等积数列”，这个常数叫做这个数列的公积．已知数列{an}是等积数列，且a1=2，公积为5，则这个数列的前n项和Sn的计算公式为：______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义映射f ：A→B，若集合A中元素x在对应法则f作用下的象为log3x，则A中元素9的象是……………………………………………………………（    ）

     A .3              B .2              C.2               D .3

    查看答案和解析>>

    同步练习册答案