【题目】某医疗研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线．
(1)写出服药后y与t之间的函数关系式；
(2)据测定，每毫升血液中含药量不少于4 μg时治疗疾病有效，假若某病人一天中第一次服药为上午7：00，问：一天中怎样安排服药时间(共4次)效果最佳？
【答案】（1）y＝
；（2）第二次服药应在11：00；第三次服药应在16：00；第四次服药应在20：30.
【解析】试题分析：（1）根据图象写出分段函数图象；（2）由题意可知，第二次服药满足－
t1＋
＝4，第三次服药，则此时血液中含药量应为前两次服药后的含药量的和，即有－t2＋－ (t2－4)＋＝4，第四次服药，则此时第一次服进的药已吸收完，血液中含药量应为第二、第三次的和，即有－ (t3－4)＋－ (t3－9)＋＝4，解得答案。
试题解析：
(1)依题意得y＝
(2)设第二次服药时在第一次服药后t1小时，则－t1＋＝4，解得t1＝4，因而第二次服药应在11：00.
设第三次服药在第一次服药后t2小时，则此时血液中含药量应为前两次服药后的含药量的和，即有－t2＋－ (t2－4)＋＝4，解得t2＝9，故第三次服药应在16：00.
设第四次服药在第一次服药后t3小时(t3>10)，则此时第一次服进的药已吸收完，血液中含药量应为第二、第三次的和，即有－ (t3－4)＋－ (t3－9)＋＝4，解得t3＝13.5，故第四次服药应在20：30.
鹰派教辅衔接教材河北教育出版社系列答案科目：高中数学 来源： 题型：
【题目】如图，已知四棱锥
的底面为矩形，D为
的中点，AC⊥平面BCC1B1．
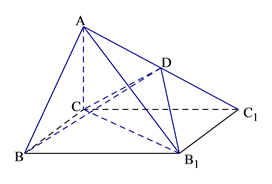
（Ⅰ）证明：AB//平面CDB1;
（Ⅱ）若AC=BC=1，BB1=
,
（1）求BD的长；
（2）求三棱锥C-DB1C1的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2016高考江苏卷】已知函数
.设
.
（1）求方程
的根;
（2）若对任意
,不等式
恒成立，求实数
的最大值；
（3）若
，函数
有且只有1个零点，求
的值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本，对高一年级的100名学生的成绩进行统计，并按
， 
， 
， 
， 
， 
分组，得到成绩分布的频率分布直方图（如图）。
（1）若规定60分以上（包括60分）为合格，计算高一年级这次竞赛的合格率；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计高一年级这次知识竞赛的学生的平均成绩；
（3）若高二年级这次竞赛的合格率为
，由以上统计数据填写下面
列联表，并问是否有
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
附：参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若有穷数列
（
是正整数），满足
即
（
是正整数，且
），就称该数列为“对称数列”。例如，数列
与数列
都是“对称数列”．
（1）已知数列
是项数为9的对称数列，且
,
,
,
,
成等差数列， 
， 
,试求
， 
， 
， 
，并求前9项和
.
（2）若
是项数为
的对称数列，且
构成首项为31，公差为
的等差数列，数列
前
项和为
，则当
为何值时， 
取到最大值？最大值为多少？
（3）设
是
项的“对称数列”，其中
是首项为1，公比为2的等比数列．求
前
项的和
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以直角坐标系的原点
为极点， 
轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，点
的极坐标为
，圆
以
为圆心，4为半径；又直线
的极坐标方程为
。
（Ⅰ）求直线
和圆
的普通方程；
（Ⅱ）试判定直线
和圆
的位置关系．若相交，则求直线
被圆
截得的弦长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在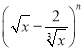
的展开式中，第5项的系数与第3项的系数之比是56：3．
（1）求展开式中的所有有理项；
（2）求展开式中系数绝对值最大的项．
（3）求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列5个命题中正确命题的个数是( )
①对于命题p：x∈R，使得x2＋x＋1<0，则綈p：x∈R，均有x2＋x＋1>0；
②m＝3是直线(m＋3)x＋my－2＝0与直线mx－6y＋5＝0互相垂直的充要条件；
③已知回归直线的斜率的估计值为1.23，样本点的中心为(4,5)，则线性回归方程为
＝1.23x＋0.08；
④若实数x，y∈[－1,1]，则满足x2＋y2≥1的概率为
；
⑤曲线y＝x2与y＝x所围成图形的面积是S＝ (x－x2)dx.
A．2 B．3
C．4 D．5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
